
Title: Stars and atoms
Author: Sir Arthur Stanley Eddington
Release date: April 8, 2024 [eBook #73362]
Language: English
Original publication: New Haven: Yale University Press
Credits: Laura Natal Rodrigues (Images generously made available by Hathi Trust Digital Library.)
Stars and Atoms

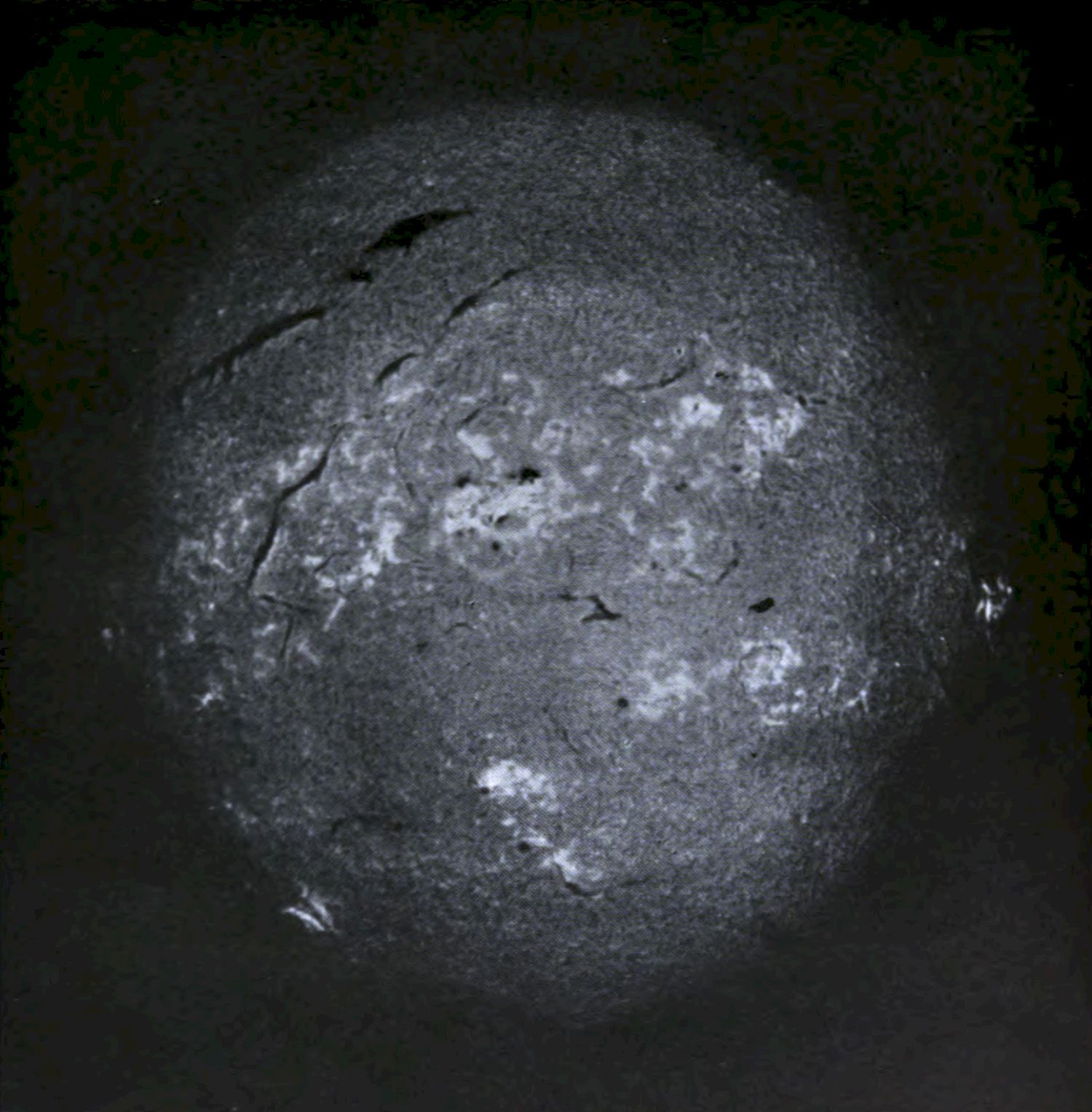
Fig. 1. THE SUN. Hydrogen photograph
BY
A. S. EDDINGTON
M.A., D.Sc., LL.D., F.R.S., Plumian Professor of Astronomy
in the University of Cambridge
NEW HAVEN: YALE UNIVERSITY PRESS
LONDON: HUMPHREY MILFORD, OXFORD UNIVERSITY PRESS
1927
[Pg 5]
‘STARS and Atoms’ was the title of an Evening Discourse given at the meeting of the British Association in Oxford in August 1926. In adapting it for publication the restrictions of a time limit are removed, and accordingly it appears in this book as three lectures. Earlier in the year I had given a course of three lectures in King’s College, London, on the same topics; these have been combined with the Oxford lecture and are the origin of most of the additions.
A full account of the subject, including the mathematical theory, is given in my larger book, The Internal Constitution of the Stars (Camb. Univ. Press, 1926). Here I only aim at exposition of some of the leading ideas and results.
The advance in our knowledge of atoms and radiation has led to many interesting developments in astronomy; and reciprocally the study of matter in the extreme conditions prevailing in stars and nebulae has played no mean part in the progress of atomic physics. This is the general theme of the lectures. Selection has been made of the advances and discoveries which admit of comparatively elementary exposition; but it is often necessary to demand from the reader a concentration of thought which, it is hoped, will be repaid by the fascination of the subject. The treatment was meant to be discursive rather than systematic; but habits of mind refuse to be suppressed entirely and a certain amount of system has crept in. In these problems where our thought fluctuates continually from the excessively great to the excessively small, from the star to the atom and back to the star, the story of progress is rich in variety; if it has not lost too much in [Pg 6] the telling, it should convey in full measure the delights—and the troubles—of scientific investigation in all its phases.
Temperatures are expressed throughout in degrees Centigrade. The English billion, trillion, &c. (1012, 1018, &c.) are used.
A. S. E.
| FIG. |
| 1. The Sun. Hydrogen Spectroheliogram. (J. Evershed) |
| 2. Solar Vortices. Hydrogen Spectroheliogram. (Mount Wilson Observatory) |
| 3. Tracks of Alpha Particles (helium atoms). (C. T. R. Wilson) |
| 4. Tracks of Beta Particles (electrons). (C. T. R. Wilson) |
| 5. Ionization by X-rays. (C. T. R. Wilson) |
| 6. Ions produced by Collision of a Beta particle. (C. T. R. Wilson) |
| 7. The Mass-luminosity Curve. |
| 8. The Ring Nebula in Lyra. Slitless Spectrogram. (W. H. Wright) |
| 9. Flash Spectrum of Chromosphere showing Head of the Balmer Series. (British Eclipse Expedition, 14 Jan. 1926) |
| 10. Solar Prominence. (British Eclipse Expedition, 29 May 1919) |
| 11. Star Cluster ω Centauri. (Cape Observatory) |
[Pg 9]
THE sun belongs to a system containing some 3,000 million stars. The stars are globes comparable in size with the sun, that is to say, of the order of a million miles in diameter. The space for their accommodation is on the most lavish scale. Imagine thirty cricket balls roaming the whole interior of the earth; the stars roaming the heavens are just as little crowded and run as little risk of collision as the cricket balls. We marvel at the grandeur of the stellar system. But this probably is not the limit. Evidence is growing that the spiral nebulae are ‘island universes’ outside our own stellar system. It may well be that our survey covers only one unit of a vaster organization.
A drop of water contains several thousand million million million atoms. Each atom is about one hundred-millionth of an inch in diameter. Here we marvel at the minute delicacy of the workmanship. But this is not the limit. Within the atom are the much smaller electrons pursuing orbits, like planets round the sun, in a space which relatively to their size is no less roomy than the solar system.
Nearly midway in scale between the atom and the star there is another structure no less marvellous—the human body. Man is slightly nearer to the atom than to the star. About 1027 atoms build his body; about 1028 human bodies constitute enough material to build a star.
From his central position man can survey the grandest works of Nature with the astronomer, or the minutest works with the physicist. To-night I ask you to look both ways. For the road to a knowledge of the stars [Pg 10] leads through the atom; and important knowledge of the atom has been reached through the stars.
The star most familiar to us is the sun. Astronomically speaking, it is close at hand. We can measure its size, weigh it, take its temperature, and so on, more easily than the other stars. We can take photographs of its surface, whereas the other stars are so distant that the largest telescope in the world does not magnify them into anything more than points of light. Figs. 1 and 2[1] show recent pictures of the sun’s surface. No doubt the stars in general would show similar features if they were near enough to be examined.
I must first explain that these are not the ordinary photographs. Simple photographs show very well the dark blotches called sunspots, but otherwise they are rather flat and uninteresting. The pictures here shown were taken with a spectroheliograph, an instrument which looks out for light of just one variety (wave-length) and ignores all the rest. The ultimate effect of this selection is that the instrument sorts out the different levels in the sun’s atmosphere and shows what is going on at one level, instead of giving a single blurred impression of all levels superposed. Fig. 2, which refers to a high level, gives a wonderful picture of whirlwinds and commotion. I think that the solar meteorologists would be likely to describe these vortices in terms not unfamiliar to us—‘A deep depression with secondaries is approaching, and a renewal of unsettled conditions is probable.’ However that may be, there is always one safe weather forecast on the sun; cyclone or anticyclone, the temperature will be very warm—about 6,000° in fact.

Fig. 2. THE SUN. Hydrogen photograph
[Pg 11]
But just now I do not wish to linger over the surface layers or atmosphere of the sun. A great many new and interesting discoveries have recently been made in this region, and much of the new knowledge is very germane to my subject of ‘Stars and Atoms’. But personally I am more at home underneath the surface, and I am in a hurry to dive below. Therefore with this brief glance at the scenery that we pass we shall plunge into the deep interior—where the eye cannot penetrate, but where it is yet possible by scientific reasoning to learn a great deal about the conditions.
By mathematical methods it is possible to work out how fast the pressure increases as we go down into the sun, and how fast the temperature must increase to withstand the pressure. The architect can work out the stresses inside the piers of his building; he does not need to bore holes in them. Likewise the astronomer can work out the stress or pressure at points inside the sun without boring a hole. Perhaps it is more surprising that the temperature can be found by pure calculation. It is natural that you should feel rather sceptical about our claim that we know how hot it is in the very middle of a star—and you may be still more sceptical when I divulge the actual figures! Therefore I had better describe the method as far as I can. I shall not attempt to go into detail, but I hope to show you that there is a clue which might be followed up by appropriate mathematical methods.
I must premise that the heat of a gas is chiefly the energy of motion [Pg 12] of its particles hastening in all directions and tending to scatter apart. It is this which gives a gas its elasticity or expansive force; the elasticity of a gas is well known to every one through its practical application in a pneumatic tyre. Now imagine yourself at some point deep down in the star where you can look upwards towards the surface or downwards towards the centre. Wherever you are, a certain condition of balance must be reached; on the one hand there is the weight of all the layers above you pressing downwards and trying to squeeze closer the gas beneath; on the other hand there is the elasticity of the gas below you trying to expand and force the superincumbent layers outwards. Since neither one thing nor the other happens and the star remains practically unchanged for hundreds of years, we must infer that the two tendencies just balance. At each point the elasticity of the gas must be just enough to balance the weight of the layers above; and since it is the heat which furnishes the elasticity, this requirement settles how much heat the gas must have. And so we find the degree of heat or temperature at each point.
The same thing can be expressed a little differently. As before, fix attention on a certain point in a star and consider how the matter above it is supported. If it were not supported it would fall to the centre under the attractive force of gravitation. The support is given by a succession of minute blows delivered by the particles underneath; we have seen that their heat energy causes them to move in all directions, and they keep on striking the matter above. Each blow gives a slight boost upwards, and the whole succession of blows supports the upper material in shuttlecock fashion. (This process is not confined to the stars; for instance, it is in this way that a motor car is [Pg 13] supported by its tyres.) An increase of temperature would mean an increase of activity of the particles, and therefore an increase in the rapidity and strength of the blows. Evidently we have to assign a temperature such that the sum total of the blows is neither too great nor too small to keep the upper material steadily supported. That in principle is our method of calculating the temperature.
One obvious difficulty arises, The whole supporting force will depend not only on the activity of the particles (temperature) but also on the number of them (density). Initially we do not know the density of the matter at an arbitrary point deep within the sun. It is in this connexion that the ingenuity of the mathematician is required. He has a definite amount of matter to play with, viz. the known mass of the sun; so the more he uses in one part of the globe the less he will have to spare for other parts. He might say to himself, ‘I do not want to exaggerate the temperature, so I will see if I can manage without going beyond 10,000,000°.’ That sets a limit to the activity to be ascribed to each particle; therefore when the mathematician reaches a great depth in the sun and accordingly has a heavy weight of upper material to sustain, his only resource is to use large numbers of particles to give the required total impulse. He will then find that he has used up all his particles too fast, and has nothing left to fill up the centre. Of course his structure, supported on nothing, would come tumbling down into the hollow. In that way we can prove that it is impossible to build up a permanent star of the dimensions of the sun without introducing an activity or temperature exceeding 10,000,000°. The mathematician can go a step beyond this; instead of merely finding a lower limit, he can ascertain what must be nearly the true temperature [Pg 14] distribution by taking into account the fact that the temperature must not be ‘patchy’. Heat flows from one place to another, and any patchiness would soon be evened out in an actual star. I will leave the mathematician to deal more thoroughly with these considerations, which belong to the following up of the clue; I am content if I have shown you that there is an opening for an attack on the problem.
This kind of investigation was started more than fifty years ago. It has been gradually developed and corrected, until now we believe that the results must be nearly right—that we really know how hot it is inside a star.
I mentioned just now a temperature of 6,000°; that was the temperature near the surface—the region which we actually see. There is no serious difficulty in determining this surface temperature by observation; in fact the same method is often used commercially for finding the temperature of a furnace from the outside. It is for the deep regions out of sight that the highly theoretical method of calculation is required. This 6,000° is only the marginal heat of the great solar furnace giving no idea of the terrific intensity within. Going down into the interior the temperature rises rapidly to above a million degrees, and goes on increasing until at the sun’s centre it is about 40,000,000°.
Do not imagine that 40,000,000° is a degree of heat so extreme that temperature has become meaningless. These stellar temperatures are to be taken quite literally. Heat is the energy of motion of the atoms or molecules of a substance, and temperature which indicates the degree of heat is a way of stating how fast these atoms or molecules are moving. For example, at the temperature of this room the molecules of air are rushing about with an average speed of 500 yards a second; if [Pg 15] we heated it up to 40,000,000° the speed would be just over 100 miles a second. That is nothing to be alarmed about; the astronomer is quite accustomed to speeds like that. The velocities of the stars, or of the meteors entering the earth’s atmosphere, are usually between 10 and 100 miles a second. The velocity of the earth travelling round the sun is 20 miles a second. So that for an astronomer this is the most ordinary degree of speed that could be suggested, and he naturally considers 40,000,000° a very comfortable sort of condition to deal with. And if the astronomer is not frightened by a speed of 100 miles a second, the experimental physicist is quite contemptuous of it; for he is used to handling atoms shot off from radium and similar substances with speeds of 10,000 miles a second. Accustomed as he is to watching these express atoms and testing what they are capable of doing, the physicist considers the jog-trot atoms of the stars very commonplace.
Besides the atoms rushing to and fro in all directions we have in the interior of a star great quantities of ether waves also rushing in all directions. Ether waves are called by different names according to their wave-length. The longest are the Hertzian waves used in broadcasting; then come the infra-red heat waves; next come waves of ordinary visible light; then ultra-violet photographic or chemical rays; then X-rays; then Gamma rays emitted by radio-active substances. Probably the shortest of all are the rays constituting the very penetrating radiation found in our atmosphere, which according to the investigations of Kohlhörster and Millikan are believed to reach us from interstellar space. These are all fundamentally the same but correspond to different octaves. The eye is attuned to only one octave, so that most of them are invisible; but essentially they are of the [Pg 16] same nature as visible light.
The ether waves inside a star belong to the division called X-rays. They are the same as the X-rays produced artificially in an X-ray tube. On the average they are ‘softer’ (i.e. longer) than the X-rays used in hospitals, but not softer than some of those used in laboratory experiments. Thus we have in the interior of a star something familiar and extensively studied in the laboratory.
Besides the atoms and ether waves there is a third population to join in the dance. There are multitudes of free electrons. The electron is the lightest thing known, weighing no more than ¹⁄₁₈₄₀ of the lightest atom. It is simply a charge of negative electricity wandering about alone. An atom consists of a heavy nucleus which is usually surrounded by a girdle of electrons. It is often compared to a miniature solar system, and the comparison gives a proper idea of the emptiness of an atom. The nucleus is compared to the sun, and the electrons to the planets. Each kind of atom—each chemical element—has a different quorum of planet electrons. Our own solar system with eight planets might be compared especially with the atom of oxygen which has eight circulating electrons. In terrestrial physics we usually regard the girdle or crinoline of electrons as an essential part of the atom because we rarely meet with atoms incompletely dressed; when we do meet with an atom which has lost one or two electrons from its system, we call it an ‘ion’. But in the interior of a star, owing to the great commotion going on, it would be absurd to exact such a meticulous standard of attire. All our atoms have lost a considerable proportion of their planet electrons and are therefore ions according to the strict nomenclature.
[Pg 17]
At the high temperature inside a star the battering of the particles by one another, and more especially the collision of the ether waves (X-rays) with atoms, cause electrons to be broken off and set free. These free electrons form the third population to which I have referred. For each individual the freedom is only temporary, because it will presently be captured by some other mutilated atom; but meanwhile another electron will have been broken off somewhere else to take its place in the free population. This breaking away of electrons from atoms is called ionization, and as it is extremely important in the study of the stars I will presently show you photographs of the process.
My subject is ‘Stars and Atoms’; I have already shown you photographs of a star, so I ought to show you a photograph of an atom. Nowadays that is quite easy. Since there are some trillions of atoms present in the tiniest piece of material it would be very confusing if the photograph showed them all. Happily the photograph exercises discrimination and shows only ‘express train’ atoms which flash past like meteors, ignoring all the others. We can arrange a particle of radium to shoot only a few express atoms across the field of the camera, and so have a clear picture of each of them.
Fig. 3[2] is a photograph of three or four atoms which have flashed across the field of view—giving the broad straight tracks. These are atoms of helium discharged at high speed from a radio-active substance.
I wonder if there is an under-current of suspicion in your minds that there must be something of a fake about this photograph. Are [Pg 18] these really the single atoms that are showing themselves—those infinitesimal units which not many years ago seemed to be theoretical concepts far outside any practical apprehension? I will answer that question by asking you one. You see a dirty mark on the picture. Is that somebody’s thumb? If you say Yes, then I assure you unhesitatingly that these streaks are single atoms. But if you are hypercritical and say ‘No. That is not anybody’s thumb, but it is a mark that shows that somebody’s thumb has been there’, then I must be equally cautious and say that the streak is a mark that shows where an atom has been. The photograph instead of being the impression of an atom is the impression of the impression of an atom, just as it is not the impression of a thumb but the impression of the impression of a thumb. I don’t see that it really matters that the impression is second-hand instead of first-hand. I do not think we have been guilty of any more faking than the criminologist who scatters powder over a finger-print to make it visible, or a biologist who stains his preparations with the same object. The atom in its passage leaves what we might call a ‘scent’ along its trail; and we owe to Professor C. T. R. Wilson a most ingenious device for making the scent visible. Professor Wilson’s ‘pack of hounds’ consists of water vapour which flocks to the trail and there condenses into tiny drops.
You will next want to see a photograph of an electron. That also can be managed. The broken wavy trail in Fig. 3 is an electron. Owing to its small mass the electron is more easily turned aside in its course than the heavy atom which rushes bull-headed through all obstacles. Fig. 4 shows numerous electrons, and it includes one of very high speed which on that account was able to make a straight track. Incidentally it gives away the device used for making the tracks visible, because you can see the tiny drops of water separately.
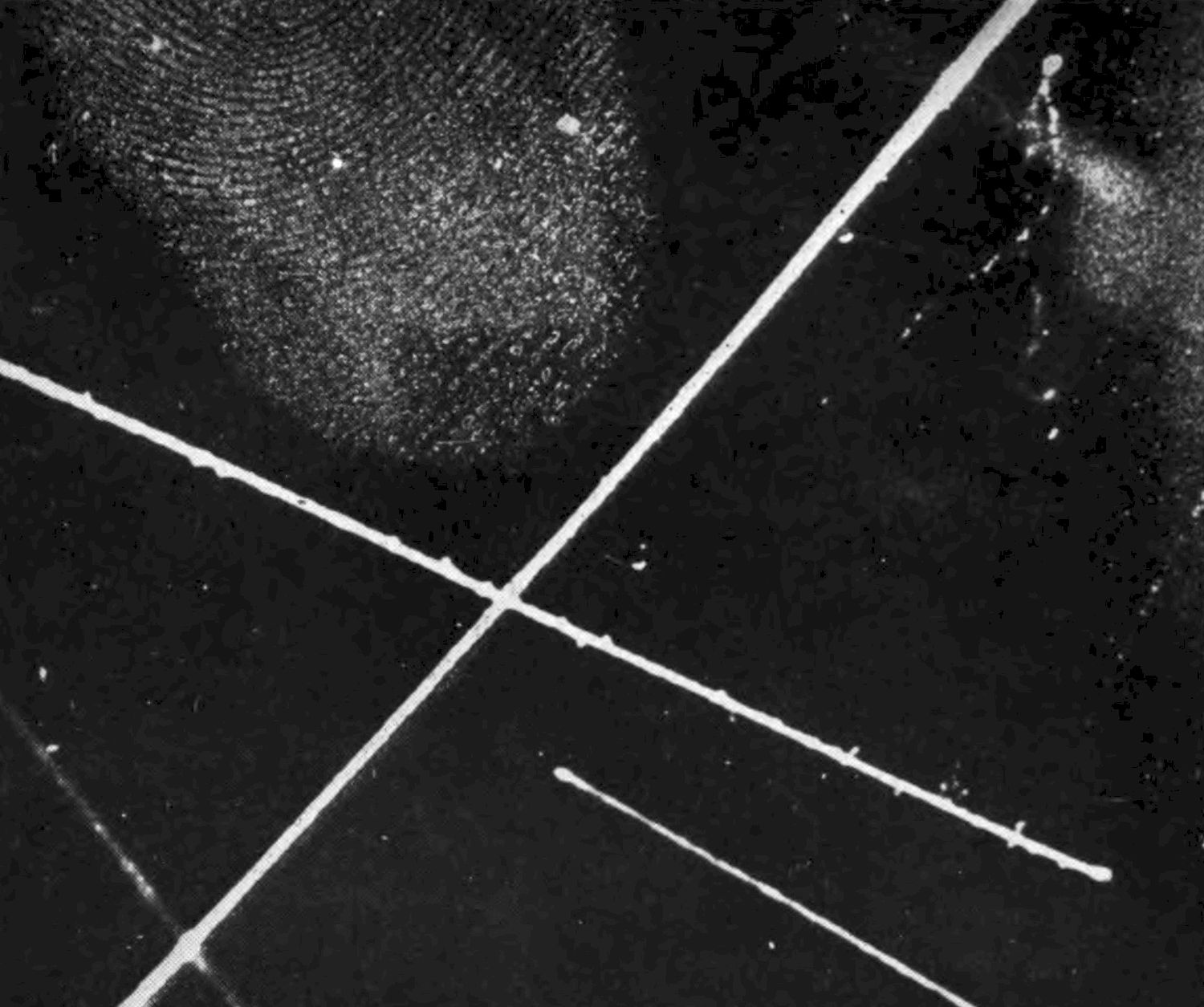
Fig. 3
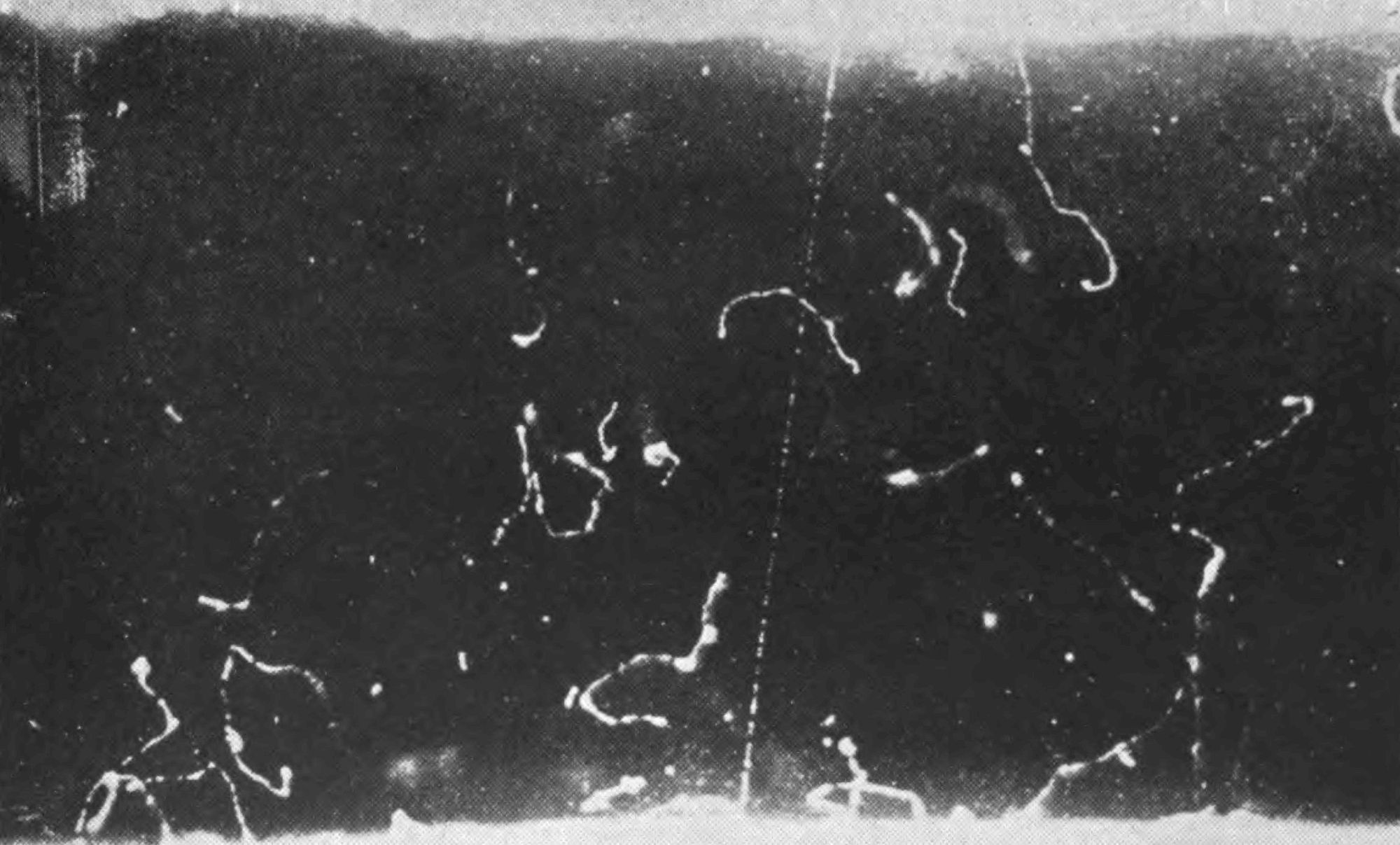
Fig. 4. FAST-MOVING ATOMS AND ELECTRONS
[Pg 19]
We have seen photographs of atoms and free electrons. Now we want a photograph of X-rays to complete the stellar population. We cannot quite manage that, but we can very nearly. Photographs by X-rays are common enough; but a photograph of X-rays is a different matter. I have already said that electrons can be broken away from atoms by X-rays colliding with them. When this happens the free electron is usually shot off with high velocity so that it is one of the express electrons which can be photographed. In Fig. 5 you see four electrons shot off in this way. You notice that they all start from points in the same line, and it does not require much imagination to see in your mind a mysterious power travelling along this line and creating the explosions. That power is the X-rays which were directed in a narrow beam along the line (from right to left) when the photograph was taken. Although the X-rays are left to your imagination, the photograph at any rate shows the process of ionization which is so important in the stellar interior—the freeing of electrons from the atoms by the incidence of X-rays. You notice that it is just a chance whether the X-ray ionizes an atom when it meets it. There are trillions of atoms lying about (of which the photograph takes no notice); but, nevertheless, the X-rays travel a long way before meeting the atom which they choose to operate on.
Finally I can show you the other method of ionizing atoms by battering of a more mechanical kind—in this case by the collision of a fast electron. In Fig. 6 a fast electron was travelling nearly horizontally, but the tiny water-drops that should mark its track are so spread out [Pg 20] that you do not at first trace the connexion. Notice that the drops occur in pairs. This is because the fast electron battered some of the atoms along its track, wrenching away an electron from each. You see at intervals along the track a broken atom and a free electron lying side by side, though you cannot tell which is which. Occasionally the original fast electron was too vigorous and there is more of a mix up, but usually you can see clearly the two fragments resulting from the smash.[3]
A cynic might remark that the interior of a star is a very safe subject to talk about because no one can go there and prove that you are wrong. I would plead in reply that at least I am not abusing the unlimited opportunity for imagination; I am only asking you to allow in the interior of the star quite homely objects and processes which can be photographed. Perhaps now you will turn round on me and say, ‘What right have you to suppose that Nature is as barren of imagination as you are? Perhaps she has hidden in the star something novel which will upset all your ideas.’ But I think that science would never have achieved much progress if it had always imagined unknown obstacles hidden round every corner. At least we may peer gingerly round the corner, and perhaps we shall find there is nothing very formidable after all. Our object in diving into the interior is not merely to admire a fantastic world with conditions transcending ordinary experience; it is to get at the inner mechanism which makes stars behave as they do. If we are to understand the surface manifestations, [Pg 21] if we are to understand why ‘one star differeth from another star in glory’, we must go below—to the engine-room—to trace the beginning of the stream of heat and energy which pours out through the surface. Finally, then, our theory will take us back to the surface and we shall be able to test by comparison with observation whether we have been badly misled. Meanwhile, although we naturally cannot prove a general negative, there is no reason to anticipate anything which our laboratory experience does not warn us of.
The X-rays in a star are the same as the X-rays experimented on in a laboratory, but they are enormously more abundant in the star. We can produce X-rays like the stellar X-rays, but we cannot produce them in anything like stellar abundance. The photograph (Fig. 5) showed a laboratory beam of X-rays which had wrenched away four electrons from different atoms; these would be speedily recaptured. In the star you must imagine the intensity multiplied many million-fold, so that electrons are being wrenched away as fast as they settle and the atoms are kept stripped almost bare. The nearly complete mutilation of the atoms is important in the study of the stars for two main reasons.
The first is this. An architect before pronouncing an opinion on the plans of a building will want to know whether the material shown in the plans is to be wood or steel or tin or paper. Similarly it would seem essential before working out details about the interior of a star to know whether it is made of heavy stuff like lead or light stuff like carbon. By means of the spectroscope we can find out a great deal about the chemical composition of the sun’s atmosphere; but it would not be fair to take this as a sample of the composition [Pg 22] of the sun as a whole. It would be very risky to make a guess at the elements preponderating in the deep interior. Thus we seem to have reached a deadlock. But now it turns out that when the atoms are thoroughly smashed up, they all behave nearly alike—at any rate in those properties with which we are concerned in astronomy. The high temperature—which we were inclined to be afraid of at first—has simplified things for us, because it has to a large extent eliminated differences between different kinds of material. The structure of a star is an unusually simple physical problem; it is at low temperatures such as we experience on the earth that matter begins to have troublesome and complicated properties. Stellar atoms are nude savages innocent of the class distinctions of our fully arrayed terrestrial atoms. We are thus able to make progress without guessing at the chemical composition of the interior. It is necessary to make one reservation, viz. that there is not an excessive proportion of hydrogen. Hydrogen has its own way of behaving; but it makes very little difference which of the other 91 elements predominate.
The other point is one about which I shall have more to say later. It is that we must realize that the atoms in the stars are mutilated fragments of the bulky atoms with extended electron systems familiar to us on the earth; and therefore the behaviour of stellar and terrestrial gases is by no means the same in regard to properties which concern the size of the atoms.
To illustrate the effect of the chemical composition of a star, we revert to the problem of the support of the upper layers by the gas underneath. At a given temperature every independent particle contributes the same amount of support no matter what its mass or chemical nature; the lighter atoms make up for their lack of mass by [Pg 23] moving more actively. This is a well-known law originally found in experimental chemistry, but now explained by the kinetic theory of Maxwell and Boltzmann. Suppose we had originally assumed the sun to be composed entirely of silver atoms and had made our calculations of temperature accordingly; afterwards we change our minds and substitute a lighter element, aluminium. A silver atom weighs just four times as much as an aluminium atom; hence we must substitute four aluminium atoms for every silver atom in order to keep the mass of the sun unchanged. But now the supporting force will everywhere be quadrupled, and all the mass will be heaved outwards by it if we make no further change. In order to keep the balance, the activity of each particle must be reduced in the ratio ¼; that means that we must assign throughout the aluminium sun temperatures ¼ of those assigned to the silver sun. Thus for unsmashed atoms a change in the assigned chemical composition makes a big change in our inference as to the internal temperature.
But if electrons are broken away from the atom these also become independent particles rendering support to the upper layers. A free electron gives just as much support as an atom does; it is of much smaller mass, but it moves about a hundred times as fast. The smashing of one silver atom provides 47 free electrons, making with the residual nucleus of the atom 48 particles in all. The aluminium atom gives 13 electrons or 14 particles in all; thus 4 aluminium atoms give 56 independent particles. The change from smashed silver to an equal mass of smashed aluminium only means a change from 48 to 56 particles, requiring a reduction of temperature by 14 per cent. We can tolerate that degree of uncertainty in our estimates of internal [Pg 24] temperature;[4] it is a great improvement on the corresponding calculation for unsmashed atoms which was uncertain by a factor 4.
Besides bringing closer together the results for different varieties of chemical constitution, ionization by increasing the number of supporting particles lowers the calculated temperatures considerably. It is sometimes thought that the exceedingly high temperature assigned to the interior of a star is a modern sensationalism. That is not so. The early investigators, who neglected both ionization and radiation pressure, assigned much higher temperatures than those now accepted.
The stars differ from one another in mass, that is to say, in the quantity of material gathered together to form them; but the differences are not so large as we might have expected from the great variety in brightness. We cannot always find out the mass of a star, but there are a fair number of stars for which the mass has been determined by astronomical measurements. The mass of the sun is—I will write it on the blackboard—
2000000000000000000000000000 tons
I hope I have counted the 0’s rightly, though I dare say you would not mind much if there were one or two too many or too few. But Nature does mind. When she made the stars she evidently attached great importance to getting the number of 0’s right. She has an idea that a star should contain a particular amount of material. Of course she allows what the officials at the mint would call a ‘remedy’. She may even pass a star with one 0 too many and give us an exceptionally large star, or with one 0 too few, giving a very small star. But these deviations are rare, and a mistake of two 0’s is almost unheard of. Usually she adheres much more closely to her pattern.
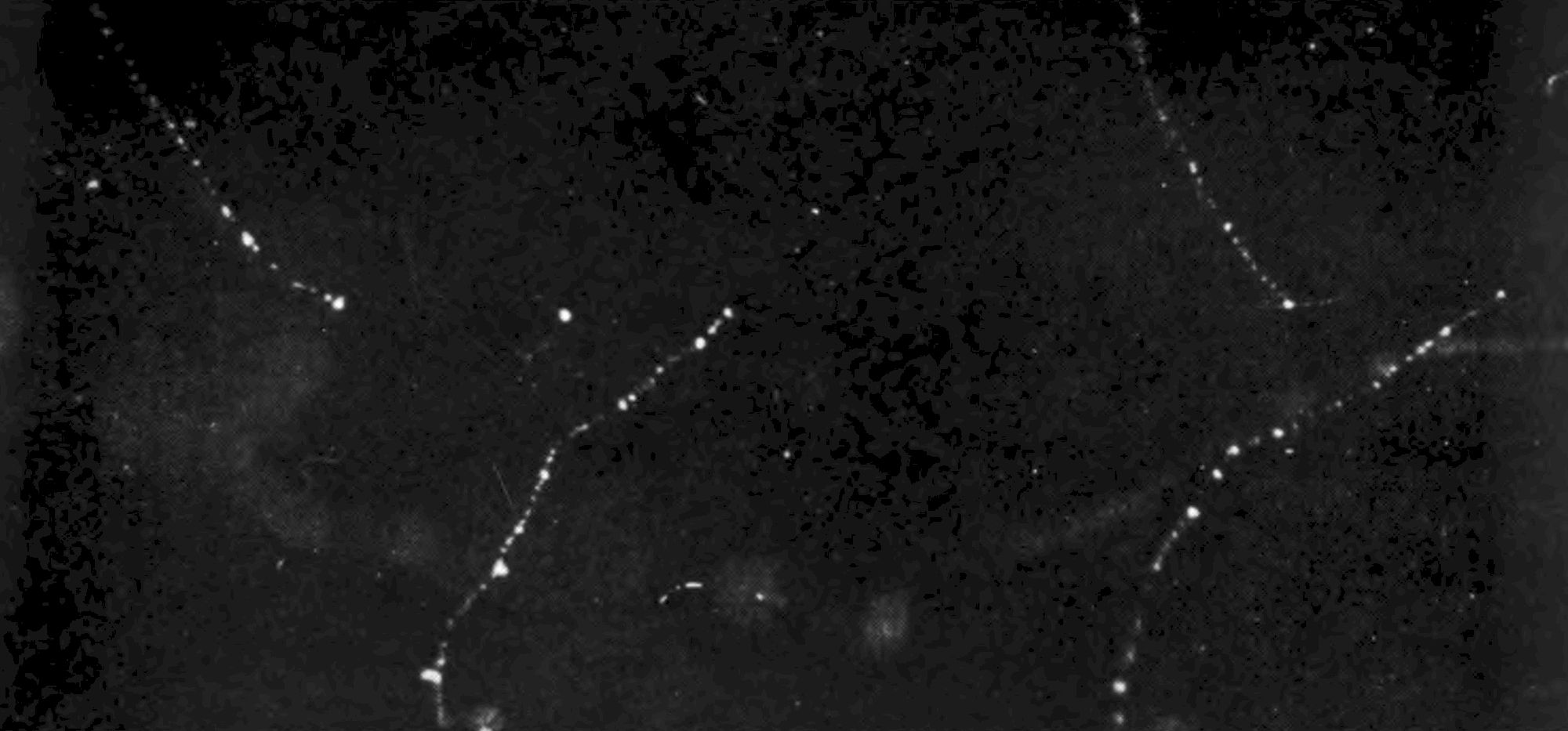
Fig. 5. IONIZATION BY X-RAYS

Fig. 6. IONIZATION BY COLLISION
[Pg 25]
How does Nature keep count of the 0’s? It seems clear that there must be something inside the star itself which keeps check and, so to speak, makes a warning protest as soon as the right amount of material has been gathered together. We think we know how it is done. You remember the ether waves inside the star. These are trying to escape outwards and they exert a pressure on the matter which is caging them in. This outward force, if it is sufficiently powerful to be worth considering in comparison with other forces, must be taken into account in any study of the equilibrium or stability of the star. Now in all small globes this force is quite trivial; but its importance increases with the mass of the globe, and it is calculated that at just about the above mass it reaches equal status with the other forces governing the equilibrium of the star. If we had never seen the stars and were simply considering as a curious problem how big a globe of matter could possibly hold together, we could calculate that there would be no difficulty up to about two thousand quadrillion tons; but beyond that the conditions are entirely altered and this new force begins to take control of the situation. Here, I am afraid, strict calculation stops, and no one has yet been able to calculate what the new force will do with the star when it does take control. But it can scarcely be an accident that the stars are all so near to this critical mass; and so I venture to conjecture the rest of the story. The new force does [Pg 26] not prohibit larger mass, but it makes it risky. It may help a moderate rotation about the axis to break up the star. Consequently larger masses will survive only rarely; for the most part stars will be kept down to the mass at which the new force first becomes a serious menace. The force of gravitation collects together nebulous and chaotic material; the force of radiation pressure chops it off into suitably sized lumps.
This force of radiation pressure is better known to many people under the name ‘pressure of light’. The term ‘radiation’ comprises all kinds of ether-waves including light, so that the meaning is the same. It was first shown theoretically and afterwards verified experimentally that light exerts a minute pressure on any object on which it falls. Theoretically it would be possible to knock a man over by turning a searchlight on him—only the searchlight would have to be excessively intense, and the man would probably be vaporized first. Pressure of light probably plays a great part in many celestial phenomena. One of the earliest suggestions was that the minute particles forming the tail of a comet are driven outwards by the pressure of sunlight, thus accounting for the fact that a comet’s tail points away from the sun. But that particular application must be considered doubtful. Inside the star the intense stream of light (or rather X-rays) is like a wind rushing outwards and distending the star.
We can now form some kind of a picture of the inside of a star—a hurly-burly of atoms, electrons, and ether-waves. Dishevelled atoms tear along at 100 miles a second, their normal array of electrons being torn from them in the scrimmage. The lost electrons are speeding 100 [Pg 27] times faster to find new resting places. Let us follow the progress of one of them. There is almost a collision as an electron approaches an atomic nucleus, but putting on speed it sweeps round in a sharp curve. Sometimes there is a side-slip at the curve, but the electron goes on with increased or reduced energy. After a thousand narrow shaves, all happening within a thousand millionth of a second, the hectic career is ended by a worse side-slip than usual. The electron is fairly caught, and attached to an atom. But scarcely has it taken up its place when an X-ray bursts into the atom. Sucking up the energy of the ray the electron darts off again on its next adventure.
I am afraid the knockabout comedy of modern atomic physics is not very tender towards our aesthetic ideals. The stately drama of stellar evolution turns out to be more like the hair-breadth escapades on the films. The music of the spheres has almost a suggestion of—jazz.
And what is the result of all this bustle? Very little. The atoms and electrons for all their hurry never get anywhere; they only change places. The ether-waves are the only part of the population which accomplish anything permanent. Although apparently darting in all directions indiscriminately, they do on the average make a slow progress outwards. There is no outward progress of the atoms and electrons; gravitation sees to that. But slowly the encaged ether-waves leak outwards as through a sieve. An ether-wave hurries from one atom to another, forwards, backwards, now absorbed, now flung out again in a new direction, losing its identity, but living again in its successor. With any luck it will in no unduly long time (ten thousand to ten million years according to the mass of the star) find itself near the boundary. It changes at the lower temperature from X-rays to [Pg 28] light-rays, being altered a little at each re-birth. At last it is so near the boundary that it can dart outside and travel forward in peace for a few hundred years. Perhaps it may in the end reach some distant world where an astronomer lies in wait to trap it in his telescope and extort from it the secrets of its birth-place.
It is the leakage that we particularly want to determine; and that is why we have to study patiently what is going on in the turbulent crowd. To put the problem in another form; the waves are urged to flow out by the temperature gradient in the star, but are hindered and turned back by their adventures with the atoms and electrons. It is the task of mathematics, aided by the laws and theories developed from a study of these same processes in the laboratory, to calculate the two factors—the factor urging and the factor hindering the outward flow—and hence to find the leakage. This calculated leakage should, of course, agree with astronomical measurements of the energy of heat and light pouring out of the star. And so finally we arrive at an observational test of the theories.
Let us consider the factor which hinders the leakage—the turning back of the ether-waves by their encounters with atoms and electrons. If we were dealing with light waves we should call this obstruction to their passage ‘opacity’, and we may conveniently use the same term for obstruction to X-rays.
We soon realize that the material of the star must be decidedly opaque. The quantity of radiation in the interior is so great that unless it were very severely confined the leakage would be much greater than the amount which we observe coming out of the stars. The following is an [Pg 29] illustration of the typical degree of opacity required to agree with the observed leakage. Let us enter the star Capella and find a region where the density is the same as that of the atmosphere around us;[5] a slab of the material only two inches thick would form a screen so opaque that only one-third of the ether-waves falling on one side would get through to the other side, the rest being absorbed in the screen. A foot or two of the material would be practically a perfect screen. If we are thinking of light-waves this seems an astonishing opacity for material as tenuous as air; but we have to remember that it is an opacity to X-rays, and the practical physicist knows well the difficulty of getting the softer kinds of X-rays to pass through even a few millimetres of air.
There is a gratifying accordance in general order of magnitude between the opacity inside the star, determined from astronomical observation of leakage, and the opacity of terrestrial substances to X-rays of more or less the same wave-length. This gives us some assurance that our theory is on the right track. But a careful comparison shows us that there is some important difference between the stellar and terrestrial opacity.
In the laboratory we find that the opacity increases very rapidly with the wave-length of the X-rays that are used. We do not find anything like the same difference in the stars although the X-rays in the cooler stars must be of considerably greater wave-length than those in the hotter stars. Also, taking care to make the comparison at the same wave-length for both, we find that the stellar opacity is less than the terrestrial opacity. We must follow up this divergence.
[Pg 30]
There is more than one way in which an atom can obstruct ether-waves, but there seems to be no doubt that for X-rays both in the stars and in the laboratory the main part of the opacity depends on the process of ionization. The ether-wave falls on an atom and its energy is sucked up by one of the planet electrons which uses it to escape from the atom and travel away at high speed. The point to notice is that in the very act of absorption the absorbing mechanism is broken, and it cannot be used again until it has been repaired. To repair it the atom must capture one of the free electrons wandering about, inducing it to take the place of the lost electron.
In the laboratory we can only produce thin streams of X-rays so that each wave-trap is only called upon to act occasionally. There is plenty of time to repair it before the next time it has a chance of catching anything; and there is practically no loss of efficiency through the traps being out of order. But in the stars the stream of X-rays is exceedingly intense. It is like an army of mice marching through your larder springing the mouse-traps as fast as you can set them. Here it is the time wasted in resetting the traps—by capturing electrons—which counts, and the amount of the catch depends almost entirely on this.
We have seen that the stellar atoms have lost most of their electrons; that means that at any moment a large proportion of the absorption traps are awaiting repair. For this reason we find a smaller opacity in the stars than in terrestrial material. The lowered opacity is simply the result of overworking the absorbing mechanisms—they have too much radiation to deal with. We can also see why the laws of stellar and terrestrial opacity are somewhat different. The rate of repair, which is the main consideration in stellar opacity, is increased by [Pg 31] compressing the material, because then the atom will not have to wait so long to meet and capture a free electron. Consequently the stellar opacity will increase with the density. In terrestrial conditions there is no advantage in accelerating the repair which will in any case be completed in sufficient time; thus terrestrial opacity is independent of the density.
The theory of stellar opacity thus reduces mainly to the theory of the capture of electrons by ionized atoms; not that this process is attended by absorption of X-rays—it is actually attended by emission—but it is the necessary preliminary to absorption. The physical theory of electron-capture is not yet fully definitive; but it is sufficiently advanced for us to make use of it provisionally in our calculations of the hindering factor in the leakage of radiation from the stars.
We do not want to tackle too difficult a problem at first, and so we shall deal with stars composed of perfect gas. If you do not like the technical phrase ‘perfect gas’ you can call it simply ‘gas’, because all the terrestrial gases that you are likely to think of are without sensible imperfection. It is only under high compression that terrestrial gases become imperfect. I should mention that there are plenty of examples of gaseous[6] stars. In many stars the material is so inflated that it is more tenuous than the air around us; for example, if you were inside Capella you would not notice the material of Capella any more than you notice the air in this room.
[Pg 32]
For gaseous stars, then, the investigation will give formulae by which, given the mass of the star, we can calculate how much energy of heat and light will leak out of it—in short, how bright it will be. In Fig. 7 a curve is drawn giving this theoretical relation between the brightness and mass of a star. Strictly speaking, there is another factor besides the mass which affects the calculated brightness; you can have two stars of the same mass, the one dense and the other puffed out, and they will not have quite the same brightness. But it turns out (rather unexpectedly) that this other factor, density, makes very little difference to the brightness, always provided that the material is not too dense to be a perfect gas. I shall therefore say no more about density in this brief summary.
Here are a few details about the scale of the diagram. The brightness is measured in magnitudes, a rather technical unit. You have to remember that stellar magnitude is like a golfer’s handicap—the bigger the number, the worse the performance. The diagram includes practically the whole range of stellar brightness; at the top -4 represents almost the brightest stars known, and at the bottom 12 is nearly the faintest limit. The difference from top to bottom is about the same as the difference between an arc light and a glow worm. The sun is near magnitude 5. These magnitudes refer, of course, to the true brightness, not to the apparent brightness affected by distance; also, what is represented here is the ‘heat brightness’ or heat intensity, which is sometimes a little different from the light intensity. Astronomical instruments have been made which measure directly the heat instead of the light received from a star. These are quite successful; but there are troublesome corrections on account of the large absorption of heat in the earth’s atmosphere, and it is in most cases easier and more accurate to infer the heat brightness from the light brightness, making allowance for the colour of the star.
[Pg 33]
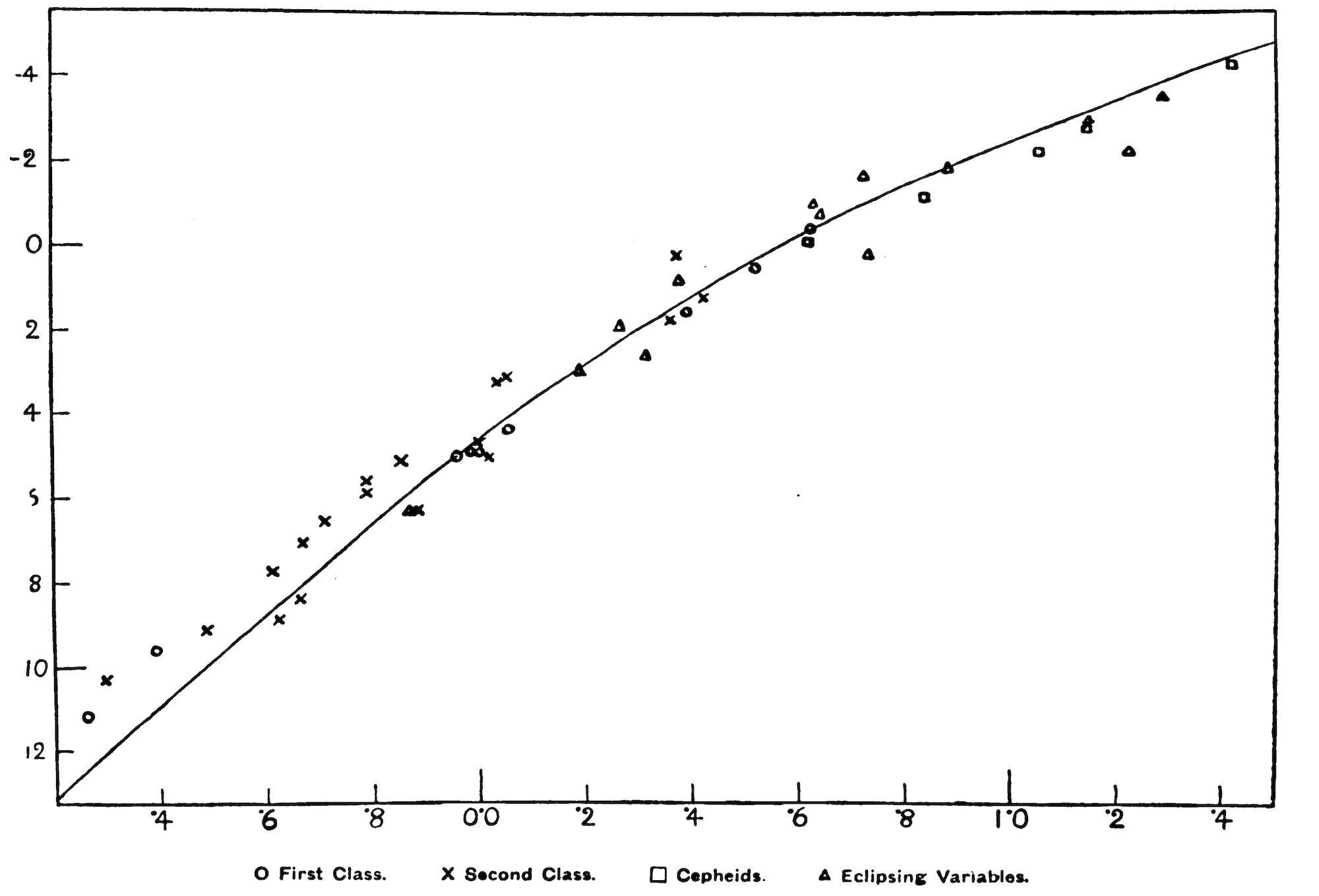
Fig. 7. The Mass-luminosity Curve.
The horizontal scale refers to mass, but it is graduated according to the logarithm of the mass. At the extreme left the mass is about ⅙ x sun, and on the extreme right about 30 x sun; there are very few stars with masses outside these limits. The sun’s mass corresponds to the division labelled 0·0.
Having obtained our theoretical curve, the first thing to do is to test it by observation. That is to say, we gather together as many stars as we can lay hands on for which both the mass and absolute brightness have been measured. We plot the corresponding points (opposite to the appropriate horizontal and vertical graduations) and see whether they fall on the curve, as they ought to do if the theory is right. There are not many stellar masses determined with much precision. Everything that is reasonably trustworthy has been included in Fig. 7. The circles, crosses, squares, and triangles refer to different kinds of data—some good, some bad, some very bad.
The circles are the most trustworthy. Let us run through them from right to left. First comes the bright component of Capella, lying beautifully on the curve—because I drew the curve through it. You see, there was one numerical constant which in the present state of our knowledge of atoms and ether-waves, &c., it was not possible to determine with any confidence from pure theory. So the curve when it was obtained was loose in one direction and could be raised or lowered. It was anchored by making it pass through the bright component of Capella which seemed the best star to trust to for this purpose. After [Pg 34] that there could be no further tampering with the curve. Continuing to the left we have the fainter component of Capella; next Sirius; then, in a bunch, two components of α Centauri (the nearest fixed star) with the Sun between them, and—lying on the curve—a circle representing the mean of six double stars in the Hyades. Finally, far on the left there are two components of a well-known double star called Krueger 60.
The observational data for testing the curve are not so extensive and not so trustworthy as we could wish; but still I think it is plain from Fig. 7 that the theory is substantially confirmed, and it really does enable us to predict the brightness of a star from its mass, or vice versa. That is a useful result, because there are thousands of stars of which we can measure the absolute brightness but not the mass, and we can now infer their masses with some confidence.
Since I have not been able to give here the details of the calculation, I should make it plain that the curve in Fig. 7 is traced by pure theory or terrestrial experiment except for the one constant determined by making it pass through Capella. We can imagine physicists working on a cloud-bound planet such as Jupiter who have never seen the stars. They should be able to deduce by the method explained on p. 25 that if there is a universe existing beyond the clouds it is likely to aggregate primarily into masses of the order a thousand quadrillion tons. They could then predict that these aggregations will be globes pouring out light and heat and that their brightness will depend on the mass in the way given by the curve in Fig. 7. All the information that we have used for the calculations would be accessible to them beneath the clouds, except that we have stolen one advantage over [Pg 35] them in utilizing the bright component of Capella. Even without this forbidden peep, present-day physical theory would enable them to assign a brightness to the invisible stellar host which would not be absurdly wrong. Unless they were wiser than us they would probably ascribe to all the stars a brilliance about ten times too great[7]—not a bad error for a first attempt at so transcendent a problem. We hope to clear up the discrepant factor 10 with further knowledge of atomic processes; meanwhile we shelve it by fixing the doubtful constant by astronomical observation.
The agreement of the observational points with the curve is remarkably close, considering the rough nature of the observational measurements; and it seems to afford a rather strong confirmation of the theory. But there is one awful confession to make—we have compared the theory with the wrong stars. At least when the comparison was first made at the beginning of 1924 no one entertained any doubt that they were the wrong stars.
We must recall that the theory was developed for stars in the condition of a perfect gas. In the right half of Fig. 7 the stars represented [Pg 36] are all diffuse stars; Capella with a mean density about equal to that of the air in this room may be taken as typical. Material of this tenuity is evidently a true gas, and in so far as these stars agree with the curve the theory is confirmed. But in the left half of the diagram we have the Sun whose material is denser than water, Krueger 60 denser than iron, and many other stars of the density usually associated with solid or liquid matter. What business have they on the curve reserved for a perfect gas? When these stars were put into the diagram it was not with any expectation that they would agree with the curve; in fact, the agreement was most annoying. Something very different was being sought for. The idea was that the theory might perhaps be trusted on its own merits with such confirmation as the diffuse stars had already afforded; then by measuring how far these dense stars fell below the curve we should have definite information as to how great a deviation from a perfect gas occurred at any given density. According to current ideas it was expected that the sun would fall three or four magnitudes below the curve, and the still denser Krueger 60 should be nearly ten magnitudes below.[8] You see that the expectation was entirely unfulfilled.
The shock was even greater than I can well indicate to you, because [Pg 37] the great drop in brightness when the star is too dense to behave as a true gas was a fundamental tenet in our conception of stellar evolution. On the strength of it the stars had been divided into two groups known as giants and dwarfs, the former being the gaseous stars and the latter the dense stars.
Two alternatives now lie before us. The first is to assume that something must have gone wrong with our theory; that the true curve for gaseous stars is not as we have drawn it, but runs high up on the left of the diagram so that the Sun, Krueger 60, &c., are at the appropriate distances below it. In short, our imaginary critic was right; Nature had hidden something unexpected inside the star and so frustrated our calculations. Well, if this were so, it would be something to have found it out by our investigations.
The other alternative is to consider this question—Is it impossible that a perfect gas should have the density of iron? The answer is rather surprising. There is no earthly reason why a perfect gas should not have a density far exceeding iron. Or it would be more accurate to say, the reason why it should not is earthly and does not apply to the stars.
The sun’s material, in spite of being denser than water, really is a perfect gas. It sounds incredible, but it must be so. The feature of a true gas is that there is plenty of room between the separate particles—a gas contains very little substance and lots of emptiness. Consequently when you squeeze it you do not have to squeeze the substance; you just squeeze out some of the waste space. But if you go on squeezing, there comes a time when you have squeezed out all the empty space; the atoms are then jammed in contact and any further compression means squeezing the substance itself, which is [Pg 38] quite a different proposition. So as you approach that density the compressibility characteristic of a gas is lost and the matter is no longer a proper gas. In a liquid the atoms are nearly in contact; that will give you an idea of the density at which the gas loses its characteristic compressibility.
The big terrestrial atoms which begin to jam at a density near that of the liquid state do not exist in the stars. The stellar atoms have been trimmed down by the breaking off of all their outer electrons. The lighter atoms are stripped to the bare nucleus—of quite insignificant size. The heavier atoms retain a few of the closer electrons, but have not much more than a hundredth of the diameter of a fully arrayed atom. Consequently we can go on squeezing ever so much more before these tiny atoms or ions jam in contact. At the density of water or even of platinum there is still any amount of room between the trimmed atoms; and waste space remains to be squeezed out as in a perfect gas.
Our mistake was that in estimating the congestion in the stellar ball-room we had forgotten that crinolines are no longer in fashion.
It was, I suppose, very blind of us not to have foreseen this result, considering how much attention we had been paying to the mutilation of the atoms in other branches of the investigation. By a roundabout route we have reached a conclusion which is really very obvious. And so we conclude that the stars on the left of the diagram are after all not the ‘wrong’ stars. The sun and other dense stars are on the perfect gas curve because their material is perfect gas. Careful investigation has shown that in the small stars on the extreme left of Fig. 7 the electric charges of the atoms and electrons bring about a [Pg 39] slight deviation from the ordinary laws of a gas; it has been shown by R. H. Fowler that the effect is to make the gas not imperfect but superperfect—it is more easily compressed than an ordinary gas. You will notice that on the average the stars run a little above the curve on the left of Fig. 7. It is probable that the deviation is genuine and is partly due to superperfection of the gas; we have already seen that imperfection would have brought them below the curve.
Even at the density of platinum there is plenty of waste space, so that in the stars we might go on squeezing stellar matter to a density transcending anything known on the earth. But that’s another story—I will tell it later on.
The general agreement between the observed and predicted brightness of the stars of various masses is the main test of the correctness of our theories of their internal constitution. The incidence of their masses in a range which is especially critical for radiation pressure is also valuable confirmation. It would be an exaggeration to claim that this limited success is a proof that we have reached the truth about the stellar interior. It is not a proof, but it is an encouragement to work farther along the line of thought which we have been pursuing. The tangle is beginning to loosen. The more optimistic may assume that it is now straightened out; the more cautious will make ready for the next knot. The one reason for thinking that the real truth cannot be so very far away is that in the interior of a star, if anywhere, the problem of matter is reduced to its utmost simplicity; and the astronomer is engaged on what is essentially a less ambitious problem than that of the terrestrial physicist to whom matter always appears in the guise [Pg 40] of electron systems of the most complex organization.
We have taken the present-day theories of physics and pressed them to their remotest conclusions. There is no dogmatic intention in this; it is the best means we have of testing them and revealing their weaknesses if any.
In ancient days two aviators procured to themselves wings. Daedalus flew safely through the middle air and was duly honoured on his landing. Icarus soared upwards to the sun till the wax melted which bound his wings and his flight ended in fiasco. In weighing their achievements, there is something to be said for Icarus. The classical authorities tell us that he was only ‘doing a stunt’, but I prefer to think of him as the man who brought to light a serious constructional defect in the flying-machines of his day. So, too, in Science. Cautious Daedalus will apply his theories where he feels confident they will safely go; but by his excess of caution their hidden weaknesses remain undiscovered. Icarus will strain his theories to the breaking-point till the weak joints gape. For the mere adventure? Perhaps partly; that is human nature. But if he is destined not yet to reach the sun and solve finally the riddle of its constitution, we may at least hope to learn from his journey some hints to build a better machine.
[Pg 41]
IT will help us to appreciate the astronomical significance of what we have learnt in the previous lecture if we turn from the general to the particular and see how it applies to individual stars. I will take two stars round which centre stories of special interest, and relate the history of our knowledge of them.
This is a detective story, which we might call ‘The Missing Word and the False Clue’.
In astronomy, unlike many sciences, we cannot handle and probe the objects of our study; we have to wait passively and receive and decode the messages that they send to us. The whole of our information about the stars comes to us along rays of light; we watch and try to understand their signals. There are some stars which seem to be sending us a regular series of dots and dashes—like the intermittent light from a lighthouse. We cannot translate this as a morse code; nevertheless, by careful measurement we disentangle a great deal of information from the messages. The star Algol is the most famous of these ‘variable stars’. We learn from the signals that it is really two stars revolving round each other. Sometimes the brighter of the two stars is hidden, giving a deep eclipse or ‘dash’; sometimes the faint star is hidden, giving a ‘dot’. This recurs in a period of 2 days 21 hours—the period of revolution of the two stars.
There was a great deal more information in the message, but it was [Pg 42] rather tantalizing. There was, so to speak, just one word missing. If we could supply that word the message would give full and accurate particulars as to the size of the system—the diameters and masses of the two components, their absolute brightness, the distance between them, their distance from the sun. Lacking the word the message told us nothing really definite about any of these things.
In these circumstances astronomers would scarcely have been human if they had not tried to guess the missing word. The word should have told us how much bigger the bright star was than the fainter, that is to say, the ratio of the masses of the two stars. Some of the less famous variable stars give us complete messages. (These could accordingly be used for testing the relation of mass and absolute brightness, and are represented by triangles in Fig. 7.) The difficulty about Algol arose from the excessive brightness of the bright component which swamped and made illegible the more delicate signals from the faint component. From the other systems we could find the most usual value of the mass ratio, and base on that a guess as to its probable value for Algol. Different authorities preferred slightly different estimates, but the general judgement was that in systems like Algol the bright component is twice as massive as the faint component. And so the missing word was assumed to be ‘two’; on this assumption the various dimensions of the system were worked out and came to be generally accepted as near the truth. That was sixteen years ago.[9]
In this way the sense of the message was made out to be that the brighter star had a radius of 1,100,000 kilometres (one and a half times the sun’s radius), that it had half the mass of the sun, and [Pg 43] thirty times the sun’s light-power, &c. It will be seen at once that this will not fit our curve in Fig. 7; a star of half the sun’s mass ought to be very much fainter than the sun. It was rather disconcerting to find so famous a star protesting against the theory; but after all the theory is to be tested by comparison with facts and not with guesses, and the theory might well have a sounder basis than the conjecture as to the missing word. Moreover, the spectral type of Algol is one that is not usually associated with low mass, and this cast some suspicion on the accepted results.
If we are willing to trust the theory given in the last lecture we can do without the missing word. Or, to put it another way, we can try in succession various guesses instead of ‘two’ until we reach one that gives the bright component a mass and luminosity agreeing with the curve in Fig. 7. The guess ‘two’ gives, as we have seen, a point which falls a long way from the curve. Alter the guess to ‘three’ and recalculate the mass and brightness on this assumption; the corresponding point is now somewhat nearer to the curve. Continue with ‘four’, ‘five’, &c.; if the point crosses the curve we know that we have gone too far and must take an intermediate value in order to reach the desired agreement. This was done in November 1925, and it appeared that the missing word must be ‘five’, not ‘two’—a rather startling change. And now the message ran—
Radius of bright component = 2,140,000 kilometres.
Mass of bright component = 4·3 x sun’s mass.
If you compare these with the original figures you will see that there is a great alteration. The star is now assigned a large mass much more appropriate to a B-type star. It also turns out that Algol is more than a hundred times as bright as the sun; and its parallax is [Pg 44] 0·028"—twice the distance previously supposed.
At the time there seemed little likelihood that these conclusions could be tested. Possibly the prediction as to the parallax might be proved or disproved by a trigonometrical determination; but it is so small as to be almost out of range of reasonably accurate measurement. We could only adopt a ‘take it or leave it’ attitude—‘If you accept the theory, this is what Algol is like; if you distrust the theory, these results are of no interest to you.’
But meanwhile two astronomers at Ann Arbor Observatory had been making a search for the missing word by a remarkable new method. They had in fact found the word and published it a year before, but it had not become widely known. If a star is rotating, one edge or ‘limb’ is coming towards us and the other going away from us. We can measure speeds towards us or away from us by means of the Doppler effect on the spectrum, obtaining a definite result in miles per second. Thus we can and do measure the equatorial speed of rotation of the sun by observing first the east limb then the west limb and taking the difference of velocity shown. That is all very well on the sun, where you can cover up the disk except the special part that you want to observe; but how can you cover up part of a star when a star is a mere point of light? You cannot; but in Algol the covering up is done for you. The faint component is your screen. As it passes in front of the bright star there is a moment when it leaves a thin crescent showing on the east and another moment when a thin crescent on the west is uncovered. Of course, the star is too far away for you actually to see the crescent shape, but at these moments you receive light from [Pg 45] the crescents only, the rest of the disk being hidden. By seizing these moments you can make the measurements just as though you had manipulated the screen yourself. Fortunately the speed of rotation of Algol is large and so can be measured with relatively small error. Now multiply the equatorial velocity by the period of rotation;[10] that will give you the circumference of Algol. Divide by 6·28, and you have the radius.
That was the method developed by Rossiter and McLaughlin. The latter who applied it to Algol found the radius of the bright component to be
2,180,000 kilometres.
So far as can be judged his result has considerable accuracy; indeed it is probable that the radius is now better known than that of any other star except the sun. If you will now turn back to p. 44 and compare it with the value found from the theory you will see that there is cause for satisfaction. McLaughlin evaluated the other constants and dimensions of the system; these agree equally well, but that follows automatically because there was only one missing word to be supplied. In both determinations the missing word or mass ratio turned out to be 5·0.
This is not quite the end of the story. Why had the first guess at the mass ratio gone so badly wrong? We understand by now that a disparity in mass is closely associated with a disparity in brightness of the two stars. The disparity in brightness was given in Algol’s original message; it informed us that the faint component gives about [Pg 46] one-thirteenth of the light of the bright one. (At least that was how we interpreted it.) According to our curve this corresponds to a mass ratio 2½, which is not much improvement on the original guess 2. For a mass ratio 5 the companion ought to have been much fainter—in fact its light should have been undetectable. Although considerations like these could not have had much influence on the original guess, they seemed at first to reassure us that there was not very much wrong with it.
Let us call the bright component Algol A and the faint component Algol B. Some years ago a new discovery was made, namely Algol C. It was found that Algol A and B together travel in an orbit round a third star in a period of just under two years—at least they are travelling round in this period, and we must suppose that there is something present for them to revolve around. Hitherto we had believed that when Algol A was nearly hidden at the time of deepest eclipse all the remaining light must come from Algol B; but now it is clear that it belongs to Algol C, which is always shining without interference. Consequently the mass ratio 2½ is that of Algol A to Algol C. The light from Algol B is inappreciable as it should be for a mass ratio 5.[11]
The message from Algol A and B was confused, not only on account of the missing word, but because a word or two of another message from Algol C had got mixed up with it; so that even when the missing word was found to be ‘five’ and confirmed in two ways, the message was not quite coherent. In another place the message seemed to waver [Pg 47] and read ‘two-and-a-half’. The finishing step is the discovery that ‘two-and-a-half’ belongs to a different message from a previously unsuspected star, Algol C. And so it all ends happily.
The best detective is not infallible. In this story our astronomical detective made a reasonable but unsuccessful guess near the beginning of the case. He might have seen his error earlier, only there was a false clue dropped by a third party who happened to be present at the crime, which seemed to confirm the guess. This was very unlucky. But it makes all the better detective story of it.
The title of this detective story is ‘The Nonsensical Message’.
Sirius is the most conspicuous star in the sky. Naturally it was observed very often in early days, and it was used by astronomers along with other bright stars to determine time and set the clocks by. It was a clock star, as we say. But it turned out that it was not at all a good clock; it would gain steadily for some years, and then lose. In 1844 Bessel found out the cause of this irregularity; Sirius was describing an elliptic orbit. Obviously there must be something for it to move around, and so it came to be recognized that there was a dark star there which no one had ever seen. I doubt whether any one expected it would ever be seen. The Companion of Sirius was, I believe, the first invisible star to be regularly recognized. We ought not to call such a star hypothetical. The mechanical properties of matter are much more crucial than the accidental property of being visible; we do not consider a transparent pane of glass ‘hypothetical’. There was near Sirius something which exhibited the most universal mechanical [Pg 48] property of matter, namely, exerting force on neighbouring matter according to the law of gravitation. That is better evidence of the existence of a material mass than ocular evidence would be.
However, eighteen years later the Companion of Sirius was actually seen by Alvan Clark. This discovery was unique in its way; Clark was not looking at Sirius because he was interested in it, but because Sirius was a nice bright point of light with which to test the optical perfection of a large new object-glass that his firm had made. I dare say that when he saw the little point of light close to Sirius he was disappointed and tried to polish it away. However, it stayed, and proved to be the already known but hitherto unseen Companion.
The big modern telescopes easily show the star and rather spoil the romance; but as romance faded, knowledge grew, and we now know that the Companion is a star not much less massive than the sun. It has ⅘ths of the mass of the sun, but gives out only ¹⁄₃₆₀th of the sun’s light. The faintness did not particularly surprise us;[11] presumably there should be white-hot stars glowing very brightly and red-hot stars glowing feebly, with all sorts of intermediate degrees of brightness. It was assumed that the Companion was one of the feeble stars only just red hot.
In 1914 Professor Adams at the Mount Wilson Observatory found that it was not a red star. It was white—white hot. Why, then, was it not shining brilliantly? Apparently the only answer was that it must be a very small star. You see, the nature and colour of the light show that its surface must be glowing more intensely than the sun’s; but the [Pg 49] total light is only ¹⁄₃₆₀th of the sun’s; therefore the surface must be less than ¹⁄₃₆₀th of the sun’s. That makes the radius less than ¹⁄₁₉th of the sun’s radius, and brings the globe down to a size which we ordinarily associate with a planet rather than with a star. Working out the sum more accurately we find that the Companion of Sirius is a globe intermediate in size between the earth and the next larger planet Uranus. But if you are going to put a mass not much less than that of the sun into a globe not very much larger than the earth, it will be a tight squeeze. The actual density works out at 60,000 times that of water—just about a ton to the cubic inch.
We learn about the stars by receiving and interpreting the messages which their light brings to us. The message of the Companion of Sirius when it was decoded ran: ‘I am composed of material 3,000 times denser than anything you have ever come across; a ton of my material would be a little nugget that you could put in a match-box.’ What reply can one make to such a message? The reply which most of us made in 1914 was—‘Shut up. Don’t talk nonsense.’
But in 1924 the theory described in the last lecture had been developed; and you will remember that at the end it pointed to the possibility that matter in the stars might be compressed to a density much transcending our terrestrial experience. This called back to mind the strange message of the Companion of Sirius. It could no longer be dismissed as obvious nonsense. That does not mean that we could immediately assume it to be true; but it must be weighed and tested with a caution which we should not care to waste over a mere nonsense jingle.
It should be understood that it was very difficult to explain away [Pg 50] the original message as a mistake. As to the mass being ⅘ths of the sun’s mass there can be no serious doubt at all. It is one of the very best determinations of stellar mass. Moreover, it is obvious that the mass must be large if it is to sway Sirius out of its course and upset its punctuality as a clock. The determination of the radius is less direct, but it is made by a method which has had conspicuous success when applied to other stars. For example, the radius of the huge star Betelgeuse was first calculated in this way; afterwards it was found possible to measure directly the radius of Betelgeuse by means of an interferometer devised by Michelson, and the direct measurement confirmed the calculated value. Again the Companion of Sirius does not stand alone in its peculiarity. At least two other stars have sent us messages proclaiming incredibly high density; and considering our very limited opportunities for detecting this condition, there can be little doubt that these ‘white dwarfs’, as they are called, are comparatively abundant in the stellar universe.
But we do not want to trust entirely to one clue lest it prove false in some unsuspected way. Therefore in 1924 Professor Adams set to work again to apply to the message a test which ought to be crucial. Einstein’s theory of gravitation indicates that all the lines of the spectrum of a star will be slightly displaced towards the red end of the spectrum as compared with the corresponding terrestrial lines. On the sun the effect is almost too small to be detected having regard to the many causes of slight shift which have to be disentangled. To me personally Einstein’s theory gives much stronger assurance of the real existence of the effect than does the observational evidence available. Still it is a striking fact that those who have made the investigation [Pg 51] are now unanimous in their judgement that the effect really occurs on the sun, although some of them at first thought that they had evidence against it. Hitherto Einstein’s theory has been chiefly regarded by the practical astronomer as something he is asked to test; but now the theory has a chance to show its mettle by helping us to test something much more doubtful than itself. The Einstein effect is proportional to the mass divided by the radius of the star; and since the radius of the Companion of Sirius is very small (if the message is right) the effect will be very large. It should in fact be thirty times as large as on the sun. That lifts it much above all the secondary causes of shift of the lines which made the test on the sun so uncertain.
The observation is very difficult because the Companion of Sirius is faint for work of this kind, and scattered light from its overpoweringly brilliant neighbour causes much trouble. However, after a year’s effort Professor Adams made satisfactory measurements, and he found a large shift as predicted. Expressing the results in the usual unit of kilometres per second, the mean of his measurements came to 19, whilst the predicted shift was 20.
Professor Adams has thus killed two birds with one stone. He has carried out a new test of Einstein’s general theory of relativity, and he has shown that matter at least 2,000 times denser than platinum is not only possible but actually exists in the stellar universe.[13] This is the best confirmation we could have for our view that the sun with a density 1½ times that of water is still very far indeed from [Pg 52] the maximum density of stellar matter; and it is therefore entirely reasonable that we should find it behaving like a perfect gas.
I have said that the observation was exceedingly difficult. However experienced the observer, I do not think we ought to put implicit trust in a result which strains his skill to the utmost until it has been verified by others working independently. Therefore you should for the present make the usual reservations in accepting these conclusions. But science is not just a catalogue of ascertained facts about the universe; it is a mode of progress, sometimes tortuous, sometimes uncertain. And our interest in science is not merely a desire to hear the latest facts added to the collection; we like to discuss our hopes and fears, probabilities and expectations. I have told the detective story so far as it has yet unrolled itself. I do not know whether we have reached the last chapter.
It should be understood that this matter of enormous density is not supposed to be any strange substance—a new chemical element or elements. It is just ordinary matter smashed about by the high temperature and so capable of being packed more tightly—just as more people could be squeezed into a room if a few bones were broken. It is one of the features of astronomical physics that it shows us the ordinary elements of the earth in an extraordinary state—smashed or ionized to a degree that has either not been reproduced or has been reproduced with great difficulty in the laboratory. It is not only in the inaccessible interior of the star that we find matter in a state outside terrestrial experience.
[Pg 53]
Here is a picture of the Ring Nebula in Lyra (Fig. 8).[14] It is taken through a prism so that we see not one ring but a number of rings corresponding to different lines of the spectrum and representing the different kinds of atoms which are at work producing the light of the nebula. The smallest ring, which is rather faint (marked by an arrow), consists of light produced by the helium atoms in the nebula—not ordinary helium but smashed helium atoms. It was one of the great laboratory achievements of recent times when Professor A. Fowler in 1912 succeeded in battering helium atoms in a vacuum tube sufficiently to give this kind of light, already well known in the stars. Two other rings are due to hydrogen. With these three exceptions none of the rings have yet been imitated in the laboratory. For instance, we do not know what elements are producing the two brightest rings on the extreme right and left respectively.
We are sometimes asked whether any new elements show themselves in the stars which are not present or are not yet discovered on the earth. We can give fairly confidently the answer No. That, however, is not because everything seen in the stars has been identified with known terrestrial elements. The answer is in fact given not by the astronomer but by the physicist. The latter has been able to make out the orderly scheme of the elements; and it transpires that there are no gaps left for fresh elements until we come to elements of very high atomic weight, which would not be likely to rise into the atmosphere of a star and show themselves in astronomical observation. Every element carries a number, starting with hydrogen which is No. 1, and going up to uranium which is No. 92.

Fig. 8. THE RING NEBULA IN LYRA
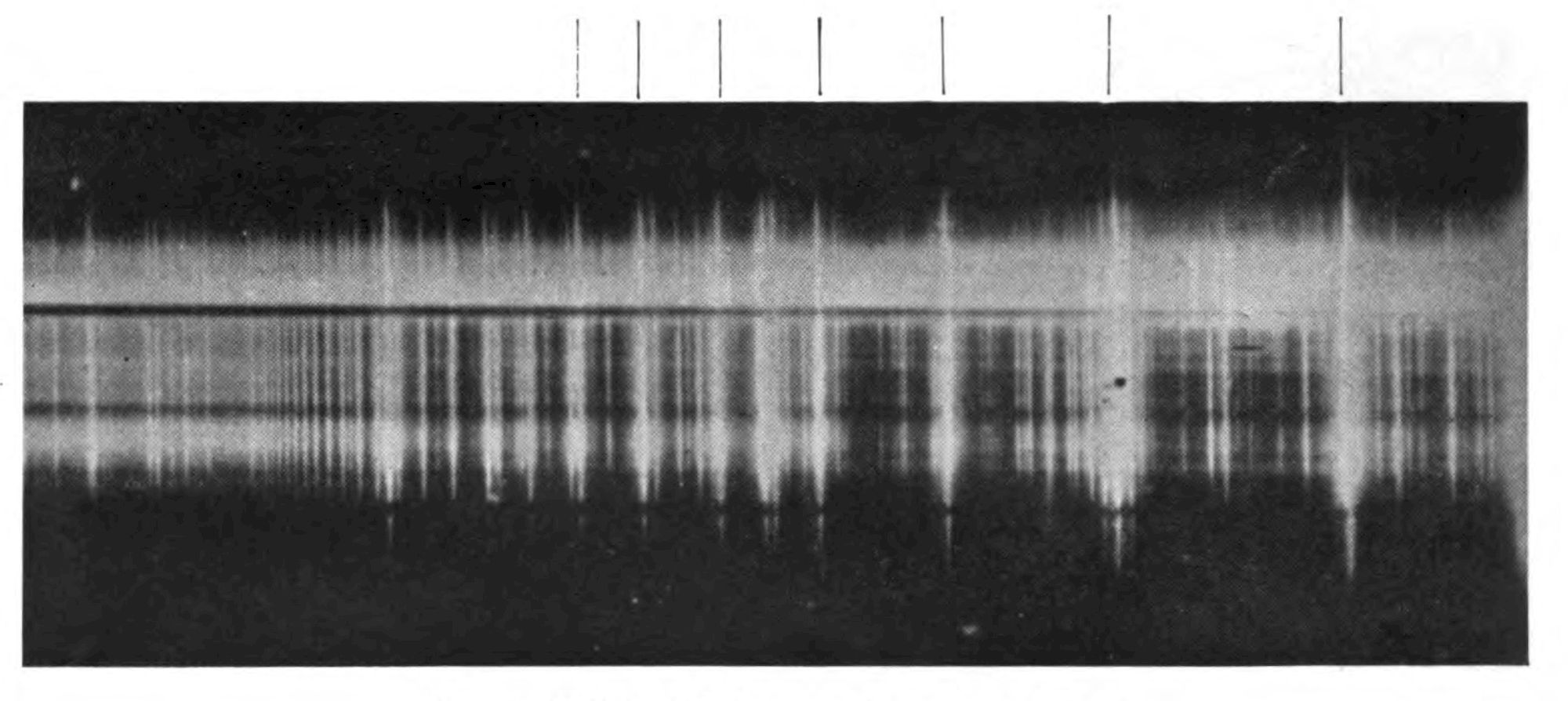
Fig. 9. HYDROGEN—THE BALMER SERIES
[Pg 54]
And what is more, the element carries its number-plate so conspicuously that a physicist is able to read it. He can, for instance, see that iron is No. 26 without having to count up how many known elements precede it. The elements have been called over by their numbers, and up to No. 84 they have all answered ‘Present’.[15]
The element helium (No. 2) was first discovered by Lockyer in the sun, and not until many years later was it found on the earth. Astrophysicists are not likely to repeat this achievement; they cannot discover new elements if there aren’t any. The unknown source of the two rings close together on the right of the photograph (a bright ring and a fainter ring) has been called nebulium. But nebulium is not a new element. It is some quite familiar element which we cannot identify because it has lost several of its electrons. An atom which has lost an electron is like a friend who has shaved off his moustache; his old acquaintances do not recognize him. We shall recognize nebulium some day. The theoretical physicists are at work trying to find laws which will determine exactly the kind of light given off by atoms in various stages of mutilation—so that it will be purely a matter of calculation to infer the atom from the light it emits. The experimental physicists are at work trying more and more powerful means of battering atoms, so that one day a terrestrial atom will be stimulated to give nebulium light. It is a great race; and I do not know which side to back. The astronomer cannot do much to help the solution of the problem he has set. I believe that if he would measure with the greatest care [Pg 55] the ratio of intensity of the two nebulium lines he would give the physicists a useful hint. He also provides another clue—though it is difficult to make anything of it—namely, the different sizes of the rings in the photograph, showing a difference in the distribution of the emitting atoms. Evidently nebulium has a fondness for the outer parts of the nebula and helium for the centre; but it is not clear what inference should be drawn from this difference in their habits.
The atoms of different elements, and atoms of the same element in different states of ionization, all have distinctive sets of lines which are shown when the light is examined through a spectroscope. Under certain conditions (as in the nebulae) these appear as bright lines; but more often they are imprinted as dark lines on a continuous background. In either case the lines enable us to identify the element, unless they happen to belong to an atom in a state of which we have had no terrestrial experience. The rash prophecy that knowledge of the composition of the heavenly bodies must be for ever beyond our reach has long been disproved; and the familiar elements, hydrogen, carbon, calcium, titanium, iron, and many others, can be recognized in the most distant parts of the universe. The thrill of this early discovery has now passed. But meanwhile stellar spectroscopy has greatly extended its scope; it is no longer chemical analysis, but physical analysis. When we meet an old acquaintance there is first the stage of recognition; the next question is ‘How are you?’ After recognizing the stellar atom we put this question, and the atom answers, ‘Quite sound’ or ‘Badly smashed’, as the case may be. Its answer conveys information as to its environment—the severity of the treatment to which it is being subjected—and hence leads to a knowledge of the conditions of [Pg 56] temperature and pressure in the object observed.
Surveying the series of stars from the coolest to the hottest, we can trace how the calcium atoms are at first whole, then singly ionized, then doubly ionized—a sign that the battering becomes more severe as the heat becomes more intense. (The last stage is indicated by the disappearance of all visible signs of calcium, because the ion with two electrons missing has no lines in the observable part of the spectrum.) The progressive change of other elements is shown in a similar way. A great advance in this study was made in 1920 by Professor M. N. Saha, who first applied the quantitative physical laws which determine the degree of ionization at any given temperature and pressure. He thereby struck out a new line in astrophysical research which has been widely developed. Thus, if we note the place in the stellar sequence where complete calcium atoms give place to atoms with one electron missing, the physical theory is able to state the corresponding temperature or pressure.[16] Saha’s methods have been improved by R. H. Fowler and E. A. Milne. One important application was to determine the surface temperatures of the hottest types of stars (12,000°—25,000°), since alternative methods available for cooler stars are not satisfactory at these high temperatures. Another rather striking result was the discovery that the pressure in the star (at the level surveyed by the spectroscope) is only ¹⁄₁₀₀₀₀th of an atmosphere; previously it had been assumed on no very definite evidence to be about the same as that of our own atmosphere.
[Pg 57]
We commonly use the method of spectrum analysis when we wish to determine which elements are present in a given mineral on the earth. It is equally trustworthy in examining the stars since it can make no difference whether the light we are studying comes from a body close at hand or has travelled to us for hundreds of years across space. But one limitation in stellar work must always be remembered. When the chemist is looking, say, for nitrogen in his mineral, he takes care to provide the conditions which according to his experience are necessary for the nitrogen spectrum to show itself. But in the stars we have to take the conditions as we find them. If nitrogen does not appear, that is no proof that nitrogen is absent; it is much more likely that the stellar atmosphere does not hit off the right conditions for the test. In the spectrum of Sirius the lines of hydrogen are exceedingly prominent and overwhelm everything else. We do not infer that Sirius is composed mainly of hydrogen; we infer instead that its surface is at a temperature near 10,000°, because it can be calculated that that is a temperature most favourable for a great development of these hydrogen lines. In the sun the most prominent spectrum is iron. We do not infer that the sun is unusually rich in iron; we infer that it is at a comparatively low temperature near 6,000° favourable for the production of the iron spectrum. At one time it was thought that the prominence of hydrogen in Sirius and of metallic elements in the sun indicated an evolution of the elements, hydrogen turning into heavier elements as the star cools from the Sirian to the solar stage. There is no ground for interpreting the observations in that way; the fading of the hydrogen spectrum and the increase of the iron spectrum would occur in any case as the result of the fall of temperature; and similar [Pg 58] spurious appearances of evolution of elements can be arranged in the laboratory.
It is rather probable that the chemical elements have much the same relative abundance in the stars that they have on the earth. All the evidence is consistent with this view; and for a few of the commoner elements there is some positive confirmation. But we are limited to the outside of the star as we are limited to the outside of the earth in computing the abundance of the elements, so that this very provisional conclusion should not be pressed unduly.
To illustrate further this kind of deduction, let us consider the spectrum shown in Fig. 9 and see what may be learnt from it. With a little trouble we can disentangle a beautifully regular series of bright lines. The marks above will assist you to pick out the first few lines of the series from the numerous other spectra mixed up with it. Noticing the diminishing spacing from right to left, you will be able to see that the series continues to the left for at least fifteen lines beyond the last one marked, the lines ultimately drawing close together and forming a ‘head’ to the series. This is the famous Balmer Series of hydrogen, and having recognized it we identify hydrogen as one of the elements present in the source of the light. But that is only the first step, and we can proceed to further inferences.
Professor Bohr’s theory of the hydrogen atom teaches us that each line of the series is emitted by an atom in a different state. These ‘states of excitation’ can be numbered consecutively, starting from the normal state of the hydrogen atom as No. 1. The light emitted in the first [Pg 59] few states comes into the part of the spectrum not reproduced here, and the first line in our picture corresponds to state No. 8. Counting to the left from this you will recognize the successive lines without much difficulty up to state No. 30. Now the successive states correspond to more and more swollen atoms, that is to say, the planet electron[17] makes a wider and wider circuit. The radius (or more strictly the semi-axis) of its orbit is proportional to the square of the number of the state, so that the orbit for state No. 30 is 900 times larger than the orbit for the normal atom No. 1. The diameter of the orbit in No. 30 is approximately a ten-thousandth of a millimetre. One inference can be drawn immediately—the spectrum shown in Fig. 9 was not produced in any terrestrial laboratory. In the highest vacuum that can be used in terrestrial spectroscopy the atoms are still too crowded to leave room for an orbit so large as this. The source must be matter so tenuous that there is vacant space for the electron to make this wide circuit without colliding with or suffering interference from other atoms. Without entering into further detail we can conclude that Fig. 9 is a spectrum of matter more rarefied than the highest vacuum known on the earth.[18]
It is interesting to notice that, whereas throughout most of the picture the lines are shown on a dark background, at the extreme left the background is bright; the change occurs just at the point where the Balmer Series comes to an end. This background of light is also due to hydrogen and it is caused in the following way. The swollen atoms in [Pg 60] state No. 30 or thereabouts are perilously near the bursting-point, so it is natural that along with them there should be atoms which have overstepped the limit and burst. They have lost their planet electrons and are occupied in catching new ones. Just as energy is required in order to wrench away an electron from an atom, so there will be superfluous energy to be got rid of when the atom tames a wild electron. This superfluous energy is radiated and forms the bright background referred to. Without entering into technicalities of the theory, we can see that it is appropriate that this light from the burst atoms should appear in the spectrum immediately beyond the lines from the most swollen atoms, since bursting is a sequel to overswelling.
Whilst you have this photograph of the Balmer Series before you I may take the opportunity of recounting the history of another famous series. In some of the hottest stars a related series of lines known as the Pickering Series was discovered in 1896. This is spaced on precisely the same regular plan, but the lines fall half way between the lines of the Balmer Series—not exactly half way because of the gradually diminishing intervals from right to left, but just where one would naturally interpolate lines in order to double their number whilst keeping the spacing regular. Unlike the Balmer Series, the Pickering Series had never been produced in any laboratory. What element was causing it? The answer seemed obvious; surely these two related series, one fitting half way between the other, must belong to different modes of vibration of the same atom, hydrogen. That seemed to be the only possible answer at the time; but we have learned more about atoms since then. We may fairly argue that the ideal simplicity of these two series indicates that they are produced by an atomic system [Pg 61] of the simplest possible type, viz. an atom with one planet electron; but it must be remembered that this condition only tells us how the atom is clothed, not what the atom is. The helium atom (or, for that matter, the uranium atom) can on occasion masquerade in the scanty attire of the hydrogen atom. Normal helium has two planet electrons; but if one of these is lost, it becomes hydrogen-like and copies the simple hydrogen system on a different scale. It is significant that the Pickering Series appears only in the very hottest stars—in conditions likely to cause loss of an electron. The difference between hydrogen and hydrogen-like helium is firstly the difference of atomic weight; the helium nucleus is four times as massive. But this scarcely affects the spectrum because both nuclei are so massive that they remain almost unshaken by the dancing electron. Secondly, the helium nucleus has a double electric charge; this is equivalent to substituting in the vibrating system a controlling spring of twice the strength. What can be more natural than that the doubled force of the spring should double the number of lines in the series without otherwise altering its plan? In this way Professor Bohr discovered the real origin of the Pickering Series; it is due to ionized helium, not to hydrogen.[19]
The heavy nucleus, whether of hydrogen or helium, remains almost unshaken by the atomic vibration—almost, but not quite. At a later date Professor A. Fowler succeeded in reproducing the Pickering Series in the laboratory and was able to measure the lines with much [Pg 62] greater accuracy than could be achieved in stellar spectroscopy; he was then able to show from his measures that the nucleus is not quite irresponsive. It was a delicate double-star problem transferred to the interior of the atom; or perhaps a closer analogy would be the mutual influence of the sun and Jupiter, because Jupiter, having a thousandth of the mass of the sun, disturbs it to about the same extent that the light electron disturbs the hydrogen nucleus. Ionized helium is a faithful copy of the hydrogen atom (on the altered scale) in everything except the ‘shake’; the shake is less than in hydrogen because the helium nucleus is still more massive and rock-like. The difference of shake throws the Pickering Series of helium and the Balmer Series of hydrogen slightly out of step with respect to one another; and by measuring this misfit Professor Fowler was able to make a very accurate determination of the shake and therefore of the mass of the electron. In this way the mass of the electron is found to be ¹⁄₁₈₄₄th of the mass of the hydrogen nucleus; this agrees well with the mass found by other methods, and the determination is probably not inferior in accuracy to any of them.
And so the clue first picked up in stars 300 light years away, followed in turn by the theoretical and the experimental physicist, leads in the end to the smallest of all things known.
Having already considered the densest matter in the universe, we now turn to consider the rarest.
In spite of great improvements in the art of exhausting vessels we are still a long way from producing a real vacuum. The atoms in a vacuum tube before it is exhausted muster a formidable number [Pg 63] containing about twenty digits. High exhaustion means knocking off five or six noughts at the end of that number; and the most strenuous efforts to knock off one more nought seem ludicrously ineffective—a mere nibbling at the huge number that must remain.
Some of the stars are extremely rarefied. Betelgeuse, for example, has a density about a thousandth that of air. We should call it a vacuum were it not contrasted with the much greater vacuosity of surrounding space. Nowadays physicists have no difficulty in producing a better vacuum than Betelgeuse; but in earlier times this star would have been regarded as a very creditable attempt at a vacuum.
The outer parts of a star, and especially the light appendages such as the solar chromosphere and corona, reach much lower densities. Also the gaseous nebulae are, as their appearance suggests, extremely tenuous. When there is space enough to put a pin’s head between adjacent atoms we can begin to talk about a ‘real vacuum.’ At the centre of the Orion nebula that degree of rarefaction is probably reached and surpassed.
A nebula has no definite boundary and the density gradually fades off. There is reason to think that the fading off becomes slow at great distances. Before we pass entirely out of the sphere of one nebula we enter the sphere of another, so that there is always some residual density in interstellar space.
I believe that, reasoning from the tailing off of the nebulae, we are in a position to make an estimate of the amount of matter remaining unaggregated in space. An ordinary region where there is no observable nebulosity is the highest vacuum existing—within the limits of the [Pg 64] stellar system at least—but there still remains about one atom in every cubic inch. It depends on our point of view whether we regard this as an amazing fullness or an amazing emptiness of space. Perhaps it is the fullness that impresses us most. The atom can find no place of real solitude within the system of the stars; wherever it goes it can nod to a colleague not more than an inch away.
Let us approach the same subject from a different angle.
In the ‘Story of Algol’ I referred to the way in which we measure the velocity of rotation of the sun. We point the spectroscope first on one limb of the sun and then on the other. Taking any one of the dark lines of the spectrum, we find that it has shifted a little between the two observations. This tells us that the material which imprinted the line was moving towards or away from us with different velocities in the two observations. That is what we expected to find; the rotation of the sun makes solar material move towards us on one side of the disk and away from us on the other side. But there are a few dark lines which do not show this change. They are in just the same position whether we observe them on the east or on the west of the sun. Clearly these cannot originate on the sun. They have been imprinted on the light after it left the sun and before it reached our telescope. We have thus discovered a medium occurring somewhere between the sun and our telescope; and as some of the lines are recognized as belonging to oxygen, we can infer that it is a medium containing oxygen.
This seems to be the beginning of a great discovery, but it ends in a bathos. It happens that we were already aware of a medium containing oxygen lying somewhere between our telescope and the sun. It is a medium essential to our existence. The terrestrial atmosphere is [Pg 65] responsible for the ‘fixed’ lines seen in the sun’s spectrum.
Just as the spectroscope can tell us that the sun is turning round (a fact already familiar to us from watching the surface markings), so it can tell us that certain stars are wandering round an orbit, and therefore are under the influence of a second star which may or may not be visible itself. But here again we sometimes find ‘fixed’ lines which do not change with the others. Therefore somewhere between the star and the telescope there exists a stationary medium which imprints these lines on the light. This time it is not the earth’s atmosphere. The lines belong to two elements, calcium and sodium, neither of which occur in the atmosphere. Moreover, the calcium is in a smashed state, having lost one of its electrons, and the conditions in our atmosphere are not such as would cause this loss. There seems to be no doubt that the medium containing the sodium and ionized calcium—and no doubt many other elements which do not show themselves—is separate from the earth and the star. It is the ‘fullness’ of interstellar space already mentioned. Light has to pass one atom per cubic inch all the way from the star to the earth, and it will pass quite enough atoms during its journey of many hundred billion miles to imprint these dark lines on its spectrum.
At first there was a rival interpretation. It was thought that the lines were produced in a cloud attached to the star—forming a kind of aureole round it. The two components travel in orbits round each other, but their orbital motion need not disturb a diffuse medium filling and surrounding the combined system. This was a very reasonable suggestion, but it could be put to the test. The test was again [Pg 66] velocity. Although either component can move periodically to and fro within the surrounding cloud of calcium and sodium, it is clear that its average approach to us or recession from us taken over a long time must agree with that of the calcium and sodium if the star is not to leave its halo behind. Professor Plaskett with the 72-inch reflector at the Dominion Observatory in British Columbia carried out this test. He found that the secular or average rate of approach of the star[20] was in general quite different from the rate shown by the fixed calcium or sodium lines. Clearly the material responsible for the fixed lines could not be an appendage of the star since it was not keeping pace with it. Plaskett went farther and showed that whereas the stars themselves had all sorts of individual velocities, the material of the fixed lines had the same or nearly the same velocity in all parts of the sky, as though it were one continuous medium throughout interstellar space. I think there can be no doubt that this research demonstrates the existence of a cosmic cloud pervading the stellar system. The fullness of interstellar space becomes a fact of observation and no longer a theoretical conjecture.
The system of the stars is floating in an ocean—not merely an ocean of space, not merely an ocean of ether, but an ocean that is so far material that one atom or thereabouts occurs in each cubic inch. It is a placid ocean without much relative motion; currents probably exist, but they are of a minor character and do not attain the high speeds commonly possessed by the stars.
Many points of interest arise, but I will only touch on one or two. Why are the calcium atoms ionized? In the calm of interstellar space [Pg 67] we seem to have passed away from the turmoil which smashed the calcium atoms in the interior of a star; so at first it seems difficult to understand why the atoms in the cloud should not be complete. However, even in the depths of space the breaking-up of the atom continues; because there is always starlight passing across space, and some of the light-waves are quite powerful enough to wrench a first or second electron away from the calcium atom. It is one of the most curious discoveries of modern physics that when a light-wave is attenuated by spreading, what it really suffers from is laziness rather than actual loss of power. What is weakened is not the power but the probability that it will display the power. A light-wave capable of bursting an atom still retains the power when it is attenuated a million-fold by spreading; only it is a million times more sparing in the exercise of the power. To put it another way, an atom exposed to the attenuated waves will on the average have to wait a million times longer before a wave chooses to explode it; but the explosion when it does occur will be of precisely the same strength however great the attenuation. This is entirely unlike the behaviour of water-waves; a wave which is at first strong enough to capsize a boat will, after spreading, become too weak. It is more like machine-gun fire which is more likely to miss a given object at greater distance but is equally destructive if it hits. The property here referred to (the quantum property) is the deepest mystery of light.
Thus in interstellar space electrons are still being torn from calcium atoms, only very infrequently. The other side of the question is the rate of repair, and in this connexion the low density of the cosmic cloud is the deciding factor. The atom has so few opportunities for repair. Roving through space the atom meets an electron only about [Pg 68] once a month, and it by no means follows that it will capture the first one it meets. Consequently very infrequent smashing will suffice to keep the majority of the atoms ionized. The smashed state of the atoms inside a star can be compared to the dilapidation of a house visited by a tornado; the smashed state in interstellar space is a dilapidation due to ordinary wear and tear coupled with excessive slackness in making repairs.
A calculation indicates that most of the calcium atoms in interstellar space have lost two electrons; these atoms do not interfere with the light and give no visible spectrum. The ‘fixed lines’ are produced by atoms temporarily in a better state of repair with only one electron missing; they cannot amount at any moment to more than one-thousandth of the whole number, but even so they will be sufficiently numerous to produce the observed absorption.
We generally think of interstellar space as excessively cold. It is quite true that any thermometer placed there would show a temperature only about 3° above the absolute zero—if it were capable of registering so low a reading. Compact matter such as a thermometer, or even matter which from the ordinary standpoint is regarded as highly diffuse, falls to this low temperature. But the rule does not apply to matter as rarefied as the interstellar cloud. Its temperature is governed by other considerations, and it will probably be not much below the surface-temperature of the hottest stars, say 15,000°. Interstellar space is at the same time excessively cold and decidedly hot.[21]
[Pg 69]
Once again we shift the scene, and now we are back in the outer parts of the sun. Fig. 10[22] shows one of the huge prominence flames which from time to time shoot out of the sun. The flame in this picture was about 120,000 miles high. It went through great changes of form and disappeared in not much more than twenty-four hours. This was rather an exceptional specimen. Smaller flames occur commonly enough; it seems that the curious black marks in Fig. 1, often looking like rifts, are really prominences seen in projection against the still brighter background of the sun. The flames consist of calcium, hydrogen, and several other elements.
We are concerned not so much with the prominences as with the layer from which they spring. The ordinary atmosphere of the sun terminates rather abruptly, but above it there is a deep though very rarefied layer called the chromosphere consisting of a few selected elements which are able to float—float, not on the top of the sun’s atmosphere, but on the sunbeams. The art of riding a sunbeam is evidently rather difficult, because only a few of the elements have the necessary skill. The most expert is calcium. The light and nimble hydrogen atom is fairly good at it, but the ponderous calcium atom does it best.
The layer of calcium suspended on the sunlight is at least 5,000 miles thick. We can observe it best when the main part of the sun is hidden by the moon in an eclipse; but the spectroheliograph enables us to study it to some extent without an eclipse.
Fig. 10. SOLAR PROMINENCE

Fig. 11. STAR CLUSTER ω CENTAURI
[Pg 70]
On the whole it is steady and quiescent, although, as the prominence flames show, it is liable to be blown sky-high by violent outbursts. The conclusions about the calcium chromosphere that I am going to describe rest on a series of remarkable researches by Professor Milne.
How does an atom float on a sunbeam? The possibility depends on the pressure of light to which we have already referred (p. 26). The sunlight travelling outwards carries a certain outward momentum; if the atom absorbs the light it absorbs also the momentum and so receives a tiny impulse outwards. This impulse enables it to recover the ground it was losing in falling towards the sun. The atoms in the chromosphere are kept floating above the sun like tiny shuttlecocks, dropping a little and then ascending again from the impulse of the light. Only those atoms which can absorb large quantities of sunlight in proportion to their weight will be able to float successfully. We must look rather closely into the mechanism of absorption of the calcium atom if we are to see why it excels the other elements.
The ordinary calcium atom has two rather loose electrons in its attendant system; the chemists express this by saying that it is a divalent element, the two loose electrons being especially important in determining the chemical behaviour. Each of these electrons possesses a mechanism for absorbing light. But under the conditions prevailing in the chromosphere one of the electrons is broken away, and the calcium atoms are in the same smashed state that gives rise to the ‘fixed lines’ in the interstellar cloud. The chromospheric calcium thus supports itself on what sunlight it can gather in with the one loose electron remaining. To part with this would be fatal; the atom [Pg 71] would no longer be able to absorb sunlight, and would drop like a stone. It is true that after two electrons are lost there are still eighteen remaining; but these are held so tightly that sunlight has no effect on them and they can only absorb shorter waves which the sun does not radiate in any quantity. The atom therefore could only save itself if it restored its main absorbing mechanism by picking up a passing electron; it has little chance of catching one in the rarefied chromosphere, so it would probably fall all the way to the sun’s surface.
There are two ways in which light can be absorbed. In one the atom absorbs so greedily that it bursts, and the electron scurries off with the surplus energy. That is the process of ionization which was shown in Fig. 5. Clearly this cannot be the process of absorption in the chromosphere because, as we have seen, the atom cannot afford to lose the electron. In the other method of absorption the atom is not quite so greedy. It does not burst, but it swells visibly. To accommodate the extra energy the electron is tossed up into a higher orbit. This method is called excitation (cf. p. 59). After remaining in the excited orbit for a little while the electron comes down again spontaneously. The process has to be repeated 20,000 times a second in order to keep the atom balanced in the chromosphere.
The point we are leading up to is, Why should calcium be able to float better than other elements? It has always seemed odd that a rather heavy element (No. 20 in order of atomic weight) should be found in these uppermost regions where one would expect only the lightest atoms. We see now that the special skill demanded is to be able to toss up an electron 20,000 times a second without ever making the fatal blunder of dropping it. That is not easy even for an atom. Calcium[23] scores [Pg 72] because it possesses a possible orbit of excitation only a little way above the normal orbit so that it can juggle the electron between these two orbits without serious risk. With most other elements the first available orbit is relatively much higher; the energy required to reach this orbit is not so very much less than the energy required to detach the electron altogether; so that we cannot very well have a continuous source of light capable of causing the orbit-jumps without sometimes overdoing it and causing loss of the electron. It is the wide difference between the energy of excitation and the energy of ionization of calcium which is so favourable; the sun is very rich in ether-waves capable of causing the first, and is almost lacking in ether-waves capable of causing the second.
The average time occupied by each performance is ¹⁄₂₀₀₀₀th of a second. This is divided into two periods. There is a period during which the atom is patiently waiting for a light-wave to run into it and throw up the electron. There is another period during which the electron revolves steadily in the higher orbit before deciding to come down again. Professor Milne has shown how to calculate from observations of the chromosphere the durations of both these periods. The first period of waiting depends on the strength of the sun’s radiation. But we focus attention especially on the second period, which is more interesting because it is a definite property of the calcium atom, having nothing to do with local circumstances. Although we measure it for ions in the sun’s chromosphere, the same result must apply to calcium ions anywhere. Milne’s result is that an electron tossed into the higher [Pg 73] orbit remains there for an average time of a hundred-millionth of a second before it spontaneously drops back again. I may add that during this brief time it makes something like a million revolutions in the upper orbit.
Perhaps this is a piece of information that you were not particularly burning to know. I do not think it can be called interesting except to those who make a hobby of atoms. But it does seem to me interesting that we should have to turn a telescope and spectroscope on the sun to find out this homely property of a substance which we handle daily. It is a kind of measurement of immense importance in physics. The theory of these atomic jumps comes under the quantum theory which is still the greatest puzzle of physical science; and it is greatly in need of guidance from observation on just such a matter as this. We can imagine what a sensation would be caused if, after a million revolutions round the sun, a planet made a jump of this kind. How eagerly we should try to determine the average interval at which such jumps occurred! The atom is rather like a solar system, and it is not the less interesting because it is on a smaller scale.
There is no prospect at present of measuring the time of relaxation of the excited calcium atom in a different way. It has, however, been found possible to determine the corresponding time for one or two other kinds of atoms by laboratory experiments. It is not necessary that the time should be at all closely the same for different elements; but laboratory measurements for hydrogen also give the period as a hundred-millionth of a second, so there is no fault to find with the astronomical determination for calcium.
The excitation of the calcium atom is performed by light of two [Pg 74] particular wave-lengths, and the atoms in the chromosphere support themselves by robbing sunlight of these two constituents. It is true that after a hundred-millionth of a second a relapse comes and the atom has to disgorge what it has appropriated; but in re-emitting the light it is as likely to send it inwards as outwards, so that the outflowing sunlight suffers more loss than it recovers. Consequently, when we view the sun through this mantle of calcium the spectrum shows gaps or dark lines at the two wave-lengths concerned. These lines are denoted by the letters H and K. They are not entirely black, and it is important to measure the residual light at the centre of the lines, because we know that it must have an intensity just strong enough to keep calcium atoms floating under solar gravity; as soon as the outflowing light is so weakened that it can support no more atoms it can suffer no further depredations, and so it emerges into outer space with this limiting intensity. The measurement gives numerical data for working out the constants of the calcium atom including the time of relaxation mentioned above.
The atoms at the top of the chromosphere rest on the weakened light which has passed through the screen below; the full sunlight would blow them away. Milne has deduced a consequence which may perhaps have a practical application in the phenomena of explosion of ‘new stars’ or novae, and in any case is curiously interesting. Owing to the Doppler effect a moving atom absorbs a rather different wave-length from a stationary atom; so that if for any cause an atom moves away from the sun it will support itself on light which is a little to one side of the deepest absorption. This light, being more intense than that which provided a balance, will make the atom recede faster. The atom’s own [Pg 75] absorption will thus gradually draw clear of the absorption of the screen below. Speaking rather metaphorically, the atom is balanced precariously on the summit of the absorption line and it is liable to topple off into the full sunlight on one side. Apparently the speed of the atom should go on increasing until it has to climb an adjacent absorption line (due perhaps to some other element); if the line is too intense to be surmounted the atom will stick part-way up, the velocity remaining fixed at a particular value. These later inferences may be rather far-fetched, but at any rate the argument indicates that there is likely to be an escape of calcium into outer space.
By Milne’s theory we can calculate the whole weight of the sun’s calcium chromosphere. Its mass is about 300 million tons. One scarcely expects to meet with such a trifling figure in astronomy. It is less than the tonnage handled by our English railways each year. I think that solar observers must feel rather hoaxed when they consider the labour that they have been induced to spend on this airy nothing. But science does not despise trifles. And astronomy can still be instructive even when, for once in a way, it descends to commonplace numbers.
This story has not much to do with atoms, and scarcely comes under the title of these lectures; but we have had occasion to allude to Betelgeuse as the famous example of a star of great size and low density, and its history is closely associated with some of the developments that we are studying.
No star has a disk large enough to be seen with our present telescopes. We can calculate that a lens or mirror of about 20 feet aperture would [Pg 76] be needed to show traces even of the largest star disk. Imagine for a moment that we have constructed an instrument of this order of size. Which would be the most hopeful star to try it on?
Perhaps Sirius suggests itself first, since it is the brightest star in the sky. But Sirius has a white-hot surface radiating very intensely, so that it is not necessary that it should have a wide expanse. Evidently we should prefer a star which, although bright, has its surface in a feebly glowing condition; then the apparent brightness must be due to large area. We need, then, a star which is both red and bright. Betelgeuse seems best to satisfy this condition. It is the brighter of the two shoulder-stars of Orion—the only conspicuous red star in the constellation. There are one or two rivals, including Antares, which might possibly be preferred; but we cannot go far wrong in turning our new instrument on Betelgeuse in the hope of finding the largest or nearly the largest star disk.
You may notice that I have paid no attention to the distances of these stars. It happens that distance is not relevant. It would be relevant if we were trying to find the star of greatest actual dimensions; but here we are considering the star which presents the largest apparent disk,[24] i.e. covers the largest area of the sky. If we were at twice our present distance from the sun, we should receive only one-quarter as much light; but the sun would look half its present size linearly, and its apparent area would be one-quarter. Thus the light per unit area of disk is unaltered by distance. Removing the sun to greater [Pg 77] and greater distance its disk will appear smaller but glowing not less intensely, until it is so far away that the disk cannot be discriminated.
By spectroscopic examination we know that Betelgeuse has a surface temperature about 3,000°. A temperature of 3,000° is not unattainable in the laboratory, and we know partly by experiment and partly by theory what is the radiating power of a surface in this state. Thus it is not difficult to compute how large an area of the sky Betelgeuse must cover in order that the area multiplied by the radiating power may give the observed brightness of Betelgeuse. The area turns out to be very small. The apparent size of Betelgeuse is that of a half-penny fifty miles away. Using a more scientific measure, the diameter of Betelgeuse predicted by this calculation is 0·051 of a second of arc.
No existing telescope can show so small a disk. Let us consider briefly how a telescope forms an image—in particular how it reproduces that detail and contrast of light and darkness which betrays that we are looking at a disk or a double star and not a blur emanating from a single point. This optical performance is called resolving power; it is not primarily a matter of magnification but of aperture, and the limit of resolution is determined by the size of aperture of the telescope.
To create a sharply defined image the telescope must not only bring light where there ought to be light, but it must also bring darkness where there ought to be darkness. The latter task is the more difficult. Light-waves tend to spread in all directions, and the telescope cannot prevent individual wavelets from straying on to parts of the picture where they have no business. But it has this one [Pg 78] remedy—for every trespassing wavelet it must send a second wavelet by a slightly longer or shorter route so as to arrive in a phase opposite to the first wavelet and cancel its effect. This is where the utility of a wide aperture arises—by affording a wider difference of route of the individual wavelets, so that those from one part of the aperture may be retarded relatively to and interfere with those from another part. A small object-glass can furnish light; it takes a big object-glass to furnish darkness in the picture.
Now we may ask ourselves whether the ordinary circular aperture is necessarily the most efficient for giving the wavelets the required path-differences. Any deviation from a symmetrical shape is likely to spoil the definition of the image—to produce wings and fringes. The image will not so closely resemble the object viewed. But on the other hand we may be able to sharpen up the tell-tale features. It does not matter how widely the image-pattern may differ from the object, provided that we can read the significance of the pattern. If we cannot reproduce a star-disk, let us try whether we can reproduce something distinctive of a star-disk.
A little reflection shows that we ought to improve matters by blocking out the middle of the object-glass, and using only the extreme regions on one side or the other. For these regions the difference of light-path of the waves is greatest, and they are the most efficient in furnishing the dark contrast needed to outline the image properly.
But if the middle of the object-glass is not going to be used, why go to the expense of manufacturing it? We are led to the idea of using two widely separated apertures, each involving a comparatively small lens or mirror. We thus arrive at an instrument after the pattern of a [Pg 79] rangefinder.
This instrument will not show us the disk of a star. If we look through it the main impression of the star image is very like what we should have seen with either aperture singly—a ‘spurious disk’ surrounded by diffraction rings. But looking attentively we see that this image is crossed by dark and bright bands which are produced by interference between the light-waves coming from the two apertures. At the centre of the image the waves from the two apertures arrive crest on crest since they have travelled symmetrically along equal paths; accordingly there is a bright band. A very little to one side the asymmetry causes the waves to arrive crest on trough, so that they cancel one another; here there is a dark band. The width of the bands decreases as the separation of the two apertures increases, and for any given separation the actual width is easily calculated.
Each point of the star’s disk is giving rise to a diffraction image with a system of bands of this kind, but so long as the disk is small compared with the finest detail of the diffraction image there is no appreciable blurring. If we continually increase the separation of the two apertures and so make the bands narrower, there comes a time when the bright bands for one part of the disk are falling on the dark bands for another part of the disk. The band system then becomes indistinct. It is a matter of mathematical calculation to determine the resultant effect of summing the band systems for each point of the disk. It can be shown that for a certain separation of the apertures the bands will disappear altogether; and beyond this separation the system should reappear though not attaining its original sharpness. The complete disappearance occurs when the diameter of the star-disk is equal to [Pg 80] 1⅕ times the width of the bands (from the centre of one bright band to the next). As already stated, the bandwidth can be calculated from the known separation of the apertures.
The observation consists in sliding apart the two apertures until the bands disappear. The diameter of the disk is inferred at once from their separation when the disappearance occurred. Although we measure the size of the disk in this way we never see the disk.
We can summarize the principle of the method in the following way. The image of a point of light seen through a telescope is not a point but a small diffraction pattern. Hence, if we look at an extended object, say Mars, the diffraction pattern will blur the fine detail of the marking on the planet. If, however, we are looking at a star which is almost a point, it is simpler to invert the idea; the object, not being an ideal point, will slightly blur the detail of the diffraction pattern. We shall only perceive the blurring if the diffraction pattern contains detail fine enough to suffer from it. Betelgeuse on account of its finite size must theoretically blur a diffraction pattern; but the ordinary diffraction disk and rings produced with the largest telescope are too coarse to show this. We create a diffraction image with finer detail by using two apertures. Theoretically we can make the detail as fine as we please by increasing the separation of the two apertures. The method accordingly consists in widening the separation until the pattern becomes fine enough to be perceptibly blurred by Betelgeuse. For a smaller star-disk the same effect of blurring would not be apparent until the detail had been made still finer by further separation of the apertures.
[Pg 81]
This method was devised long ago by Professor Michelson, but it was only in 1920 that he tried it on a large scale with a great 20-foot beam across the 100-inch reflector at Mount Wilson Observatory. After many attempts Pease and Anderson were able to show that the bright and dark bands for Betelgeuse disappeared when the apertures were separated 10 feet. The deduced diameter is 0·045 a second of arc in good enough agreement with the predicted value (p. 78). Only five or six stars have disks large enough to be measured with this instrument. It is understood that the construction of a 50-foot interferometer is contemplated; but even this will be insufficient for the great majority of the stars. We are fairly confident that the method of calculation first described gives the correct diameters of the stars, but confirmation by Michelson’s more direct method of measurement is always desirable.
To infer the actual size of the star from its apparent diameter, we must know the distance. Betelgeuse is rather a remote star and its distance cannot be measured very accurately, but the uncertainty will not change the general order of magnitude of the results. The diameter is about 300 million miles. Betelgeuse is large enough to contain the whole orbit of the earth inside it, perhaps even the orbit of Mars. Its volume is about fifty million times the volume of the sun.
There is no direct way of learning the mass of Betelgeuse because it has no companion near it whose motion it might influence. We can, however, deduce a mass from the mass-brightness relation in Fig. 7. This gives the mass equal to 35 x sun. If the result is right, Betelgeuse is one of the most massive stars—but, of course, not massive in proportion to its bulk. The mean density is about [Pg 82] one-millionth of the density of water, or not much more than one-thousandth of the density of air.[25]
There is one way in which we might have inferred that Betelgeuse is less dense than the sun, even if we had had no grounds of theory or analogy for estimating its mass. According to the modern theory of gravitation, a globe of the size of Betelgeuse and of the same mean density as the sun would have some remarkable properties:
Firstly, owing to the great intensity of its gravitation, light would be unable to escape; and any rays shot out would fall back again to the star by their own weight.
Secondly, the Einstein shift (used to test the density of the Companion of Sirius) would be so great that the spectrum would be shifted out of existence.
Thirdly, mass produces a curvature of space, and in this case the curvature would be so great that space would close up round the star, leaving us outside—that is to say, nowhere.
Except for the last consideration, it seems rather a pity that the density of Betelgeuse is so low.
It is now well realized that the stars are a very important adjunct to the physical laboratory—a sort of high-temperature annex where the behaviour of matter can be studied under greatly extended conditions. Being an astronomer, I naturally put the connexion somewhat differently and regard the physical laboratory as a low-temperature station attached to the stars. It is the laboratory conditions which should be counted abnormal. Apart from the interstellar cloud which is at the [Pg 83] moderate temperature of about 15,000°, I suppose that nine-tenths of the matter of the universe is above 1,000,000°. Under ordinary conditions—you will understand my use of the word—matter has rather simple properties. But there are in the universe exceptional regions with temperature not far removed from the absolute zero, where the physical properties of matter acquire great complexity; the ions surround themselves with complete electron systems and become the atoms of terrestrial experience. Our earth is one of these chilly places and here the strangest complications can arise. Perhaps strangest of all, some of these complications can meet together and speculate on the significance of the whole scheme.
[Pg 84]
WE have seen that spatially the scale of man is about midway between the atom and the star. I am tempted to make a similar comparison as regards time. The span of the life of a man comes perhaps midway in scale between the life of an excited atom (p. 74) and the life of a star. For those who insist on greater accuracy—though I would not like to claim accuracy for present estimates of the life of a star—I will modify this a little. As regards mass, man is rather too near to the atom and a stronger claimant for the midway position would be the hippopotamus. As regards time, man’s three score years and ten is a little too near to the stars and it would be better to substitute a butterfly.
There is one serious moral in this fantasy. We shall have to consider periods of time which appall our imagination. We fear to make such drafts on eternity. And yet the vastness of the time-scale of stellar evolution is less remote from the scale of human experience than is the minuteness of the time-scale of the processes studied in the atom.
Our approach to the ‘age of the stars’ will be devious, and certain incidental problems will detain us on the way.
The star δ Cephei is one of the variable stars. Like Algol, its fluctuating light sends us a message. But the message when it is decoded is not in the least like the message from Algol.
Let me say at once that experts differ as to the interpretation of the [Pg 85] message of δ Cephei. This is not the place to argue the matter, or to explain why I think that rival interpretations cannot be accepted. I can only tell you what is to the best of my belief the correct story. The interpretation which I follow was suggested by Plummer and Shapley. The latter in particular made it very convincing, and subsequent developments have, I think, tended to strengthen it. I would not, however, claim that all doubt is banished.
Algol turned out to be a pair of stars very close together which from time to time eclipse one another; δ Cephei is a single star which pulsates. It is a globe which swells and contracts symmetrically with a regular period of 5⅓ days. And as the globe swells and contracts causing great changes of pressure and temperature in the interior, so the issuing stream of light rises and falls in intensity and varies also in quality or colour.
There is no question of eclipses; the light signals are not in the form of ‘dots’ and ‘dashes’; and in any case the change of colour shows that there is a real change in the physical condition of the source of the light. But at first explanations always assumed that two stars were concerned, and aimed at connecting the physical changes with an orbital motion. For instance, it was suggested that the principal star in going round its orbit brushed through a resisting medium which heated its front surface; thus the light of the star varied according as the heated front surface or cooler rear surface was presented towards us. The orbital explanation has now collapsed because it is found that there is literally no room for two stars. The supposed orbit had been worked out in the usual way from spectroscopic measurements of velocity of approach and recession; later we began to learn more about the true size of stars, first by calculation, and afterwards (for a [Pg 86] few stars) by direct measurement. It turned out that the star was big and the orbit small; and the second star if it existed would have to be placed inside the principal star. This overlapping of the stars is a reductio ad absurdum of the binary hypothesis, and some other explanation must be found.
What had been taken to be the approach and recession of the star as a whole was really the approach and recession of the surface as it heaved up and down with the pulsation. The stars which vary like δ Cephei are diffuse stars enormously larger than the sun, and the total displacement measured amounts to only a fraction of the star’s radius. There is therefore no need to assume a bodily displacement of the star (orbital motion); the measures follow the oscillation of that part of the star’s surface presented towards us.
The decision that δ Cephei is a single star and not double has one immediate consequence. It means that the period of 5⅓ days is intrinsic in the star and is therefore one of the clues to its physical condition. It is a free period, not a forced period. It is important to appreciate the significance of this. The number of sunspots fluctuates from a maximum to minimum and back to maximum in a period of about 11½ years; although we do not yet understand the reason for this fluctuation, we realize that this period is something characteristic of the sun in its present state and would change if any notable change happened to the sun. At one time, however, there was some speculation as to whether the fluctuation of the sunspots might not be caused by the revolution of the planet Jupiter, which has a period not so very different; if that explanation had been tenable the 11½-year period would have been something forced on the sun from [Pg 87] without and would teach us nothing as to the properties of the sun itself. Having convinced ourselves that the light-period of δ Cephei is a free period of a single star, belonging to it in the same way that a particular note belongs to a tuning-fork, we can accept it as a valuable indicator of the constancy (or otherwise) of the star’s physical condition.
In stellar astronomy we usually feel very happy if we can determine our data—parallax, radius, mass, absolute brightness, &c.—to within 5 per cent.; but the measurement of a period offers chances of far superior accuracy. I believe that the most accurately known quantity in the whole of science (excluding pure mathematics) is the moon’s mean period, which is commonly given to twelve significant figures. The period of δ Cephei can be found to six significant figures at least. By fastening an observable period to the intrinsic conditions of a star we have secured an indicator sensitive enough to show extremely small changes. You will now guess why I am approaching ‘the age of the stars’ through the Cepheid variables. Up to the present they are the only stars known to carry a sensitive indicator, by which we might hope to test the rate of evolutionary change. We believe that δ Cephei like other stars has condensed out of a nebula, and that the condensation and contraction are still continuing. No one would expect to detect the contraction by our rough determinations of the radius even if continued for a hundred years; but the evolution must indeed be slow if an intrinsic period measurable to 1 part in 10,000,000 shows no change in a century.
It does not greatly matter whether or not we understand the nature of this intrinsic period. If a star contracts, the period of pulsation, [Pg 88] the period of rotation, or any other free period associated with it, will alter. If you prefer to follow any of the rival interpretations of the message of δ Cephei, you can make the necessary alterations in the wording of my argument, but the general verdict as to the rate of progress of evolution will be unchanged. Only if you detach the period from the star itself by going back to the old double star interpretation will the argument collapse; but I do not think any of the rival interpreters propose to do that.
It is not surprising that these pulsating stars should be regarded with special interest. Ordinary stars must be viewed respectfully like the objects in glass cases in museums; our fingers are itching to pinch them and test their resilience. Pulsating stars are like those fascinating models in the Science Museum provided with a button which can be pressed to set the machinery in motion. To be able to see the machinery of a star throbbing with activity is most instructive for the development of our knowledge.
The theory of a steady star, which was described in the first lecture, can be extended to pulsating stars; and we can calculate the free period of pulsation for a star of assigned mass and density. You will remember that we have already calculated the heat emission or brightness and compared it with observation, obtaining one satisfactory test of the truth of the theory; now we can calculate the period of pulsation and by comparing it with observation obtain another test. Owing to lack of information as to a certain constant of stellar material there is an uncertainty in the calculation represented by a factor of about 2; that is to say, we calculate two periods, one double the other, between which with any reasonable luck the true period [Pg 89] ought to lie. The observational confirmation is very good. There are sixteen Cepheid variables on which the test can be made; their periods range from 13 hours to 35 days, and they all agree with the calculated values to within the limits of accuracy expected. In a more indirect way the same confirmation is shown in Fig. 7 by the close agreement of the squares, representing Cepheid variables, with the theoretical curve.
Cepheid variables of the same period are closely similar to one another. A Cepheid of period 5⅓ days found in any part of the universe will be practically a replica of δ Cephei; in particular it will be a star of the same absolute brightness. This is a fact discovered by observation, and is not predicted by any part of the theory yet explored. The brightness, as we have seen, depends mainly on the mass; the period, on the other hand, depends mainly on the density; so that the observed relation between brightness and period involves a relation between mass and density. Presumably this relation signifies that for a given mass there is just one special density—one stage in the course of condensation of the star—at which pulsations are liable to occur; at other densities the star can only burn steadily.
This property renders the Cepheid extremely useful to astronomers. It serves as a standard candle—a source of known light-power.
In an ordinary way you cannot tell the real brightness of a light merely by looking at it. If it appears dim, that may mean either real faintness or great distance. At night time on the sea you observe many lights whose distance and real brightness you cannot estimate; [Pg 90] your judgement of the real brightness may be wrong by a factor of a quintillion if you happen to mistake Arcturus for a ship’s light. But among them you may notice a light which goes through a regular series of changes in a certain number of seconds; that tells you that it is such-and-such a lighthouse, known to project a light of so many thousand candlepower. You may now estimate with certainty how far off it is—provided, of course, that there is no fog intervening.
So, too, when we look up at the sky, most of the lights that we see might be at any distance and have any real brightness. Even the most refined measurements of parallax only succeed in locating a few of the nearer lights. But if we see a light winking in the Cepheid manner with a period of 5⅓ days, we know that it is a replica of δ Cephei and is a light of 700 sun-power. Or if the period is any other number of days we can assign the proper sun-power for that period. From this we can judge the distance. The apparent brightness, which is a combination of distance and true brightness, is measured; then it is a simple calculation to answer the question, At what distance must a light of 700 sun-power be placed in order to give the apparent brightness observed? How about interference by fog? Careful discussions have been made, and it appears that notwithstanding the cosmical cloud in interstellar space there is ordinarily no appreciable absorption or scattering of the starlight on its way to us.
With the Cepheids serving as standard candles distances in the stellar universe have been surveyed far exceeding those reached by previous methods. If the distances were merely those of the Cepheid variables themselves that would not be so important, but much more information is yielded.
[Pg 91]
Fig. 11[26] shows a famous star-cluster called ω Centauri. Amongst the thousands of stars in the cluster no less than 76 Cepheid variables have been discovered. Each is a standard candle serving to measure the distance primarily of itself but also incidentally of the great cluster in which it lies. The 76 gauges agree wonderfully among themselves, the average deviation being less than 5 per cent. By this means Shapley found the distance of the cluster to be 20,000 light years. The light messages which we receive to-day were sent from the cluster 20,000 years ago.[27]
The astronomer, more than other devotees of science, learns to appreciate the advantage of not being too near the objects he is studying. The nearer stars are all right in their way, but it is a great nuisance being in the very midst of them. For each star has to be treated singly and located at its proper distance by elaborate measurements; progress is very laborious. But when we determine the distance of this remote cluster, we secure at one scoop the distances of many thousands of stars. The distance being known, the apparent magnitudes can be turned into true magnitudes, and statistics and correlations of absolute brightness and colour can be ascertained. Even before the distance is discovered we can learn a great deal from the stars in clusters which it is impracticable to find out from less remote stars. We can see that the Cepheids are much above the average brightness and are surpassed by relatively few stars. We can ascertain that the brighter the Cepheid the longer is its period. We discover that the brightest stars of all are red.[28] And so on. There is a [Pg 92] reverse side to the picture; the tiny points of light in the distant cluster are not the most satisfactory objects to measure and analyse, and we could ill spare the nearer stars; but the fact remains that there are certain lines of stellar investigation in which remoteness proves to be an actual advantage, and we turn from the nearer stars to objects fifty thousand light years away.
About 80 globular clusters are known with distances ranging from 20,000 to 200,000 light years. Is there anything yet more remote? It has long been suspected that the spiral nebulae,[29] which seem to be exceedingly numerous, are outside our stellar system and form ‘island universes’. The evidence for this has become gradually stronger, and now is believed to be decisively confirmed. In 1924 Hubble discovered a number of Cepheid variables in the great Andromeda nebula which is the largest and presumably one of the nearest of the spirals. As soon as their periods had been determined they were available as standard candles to gauge the distance of the nebula. Their apparent magnitude was much fainter than that of the corresponding Cepheids in globular clusters, showing that they must be even more remote. Hubble has since found the distance of one or two other spirals in the same way.
With the naked eye you can see the Andromeda nebula as a faint patch of light. When you look at it you are looking back 900,000 years into the past.
[Pg 93]
The problem of providing sufficient supplies of energy to maintain the sun’s output of light and heat has often been debated by astronomers and others. In the last century it was shown by Helmholtz and Kelvin that the sun could maintain its heat for a very long time by continually shrinking. Contraction involves an approach or fall of the matter towards the centre; gravitational potential energy is thus converted and made available as heat. It was assumed that this was the sole resource since no other supply capable of yielding anything like so large an amount was known. But the supply is not unlimited, and on this hypothesis the birth of the sun must be dated not more than 20,000,000 years ago. Even at the time of which I am speaking the time-limit was found to be cramping; but Kelvin assured the geologists and biologists that they must confine their outlines of terrestrial history within this period.
About the beginning of the present century the contraction theory was in the curious position of being generally accepted and generally ignored. Whilst few ventured to dispute the hypothesis, no one seems to have had any hesitation, if it suited him, in carrying back the history of the earth or moon to a time long before the supposed era of the formation of the solar system. Lord Kelvin’s date of the creation was treated with no more respect than Archbishop Ussher’s.
The serious consequences of the hypothesis become particularly prominent when we consider the diffuse stars of high luminosity; these are prodigal of their energy and squander it a hundred or a thousand times faster than the sun. The economical sun could have subsisted [Pg 94] on its contraction energy for 20,000,000 years, but for the high luminosity stars the limit is cut down to 100,000 years. This includes most of the naked-eye stars. Dare we believe that they were formed within the last 100,000 years? Is the antiquity of man greater than that of the stars now shining? Do stars in the Andromeda nebula run their course in less time than their light takes to reach us?
It is one thing to feel a limitation of time-scale irksome, ruling out ideas and explanations which are otherwise plausible and attractive; it is another thing to produce definite evidence against the time-scale. I do not think that astronomers had in their own territory any weapon for a direct attack on the Helmholtz-Kelvin hypothesis until the Cepheid variables supplied one. To come to figures: δ Cephei emits more than 700 times as much heat as the sun. We know its mass and radius, and we can calculate without difficulty how fast the radius must contract in order to provide this heat. The required rate is one part in 40,000 per annum. Now δ Cephei was first observed carefully in 1785, so that in the time it has been under observation the radius must have changed by one part in 300 if the contraction hypothesis is right. You remember that we have in δ Cephei a very sensitive indicator of any changes occurring in it, viz. the period of pulsation; clearly changes of the above magnitude could not occur without disturbing this indicator. Does the period show any change? It is doubtful; there is perhaps sufficient evidence for a slight change, but it is not more than ¹⁄₂₀₀th of the change demanded by the contraction hypothesis.
Accepting the pulsation theory, the period should diminish 17 seconds every year—a quantity easily detectable. The actual change is not [Pg 95] more than one-tenth of a second per year. At least during the Cepheid stage the stars are drawing on some source of energy other than that provided by contraction.
On such an important question we should not like to put implicit trust in one argument alone, and we turn to the sister sciences for other and perhaps more conclusive evidence. Physical and geological investigations seem to decide definitely that the age of the earth—reckoned from an epoch which by no means goes back to its beginnings as a planet—is far greater than the Helmholtz-Kelvin estimate of the age of the solar system. It is usual to lay most stress on a determination of the age of the rocks from the uranium-lead ratio of their contents. Uranium disintegrates into lead and helium at a known rate. Since lead is unlike uranium in chemical properties the two elements would not naturally be deposited together; so that the lead found with uranium has presumably been formed by its decomposition.[30] By measuring how much lead occurs with the uranium we can determine how long ago the uranium was deposited. The age of the older rocks is found to be about 1,200 million years; lower estimates have been urged by some authorities, but none low enough to save the contraction hypothesis. The sun, of course, must be very much older than the earth and its rocks.
We seem to require a time-scale which will allow at least 10,000,000,000 years for the age of the sun; certainly we cannot abate our demands below 1,000,000,000 years. It is necessary to look for a more prolific source of energy to maintain the heat of the [Pg 96] sun and stars through this extended period. We can at once narrow down the field of search. No source of energy is of any avail unless it liberates heat in the deep interior of the star. The crux of the problem is not merely the provision for radiation but the maintenance of the internal heat which keeps the gravitating mass from collapsing. You will remember how in the first lecture we had to assign a certain amount of heat at each point in the stellar interior in order to keep the star in balance. But the internal heat is continually running away towards the cooler outside and then escaping into space as the star’s radiation. This, or its equivalent, must be put back if the star is to be kept steady—if it is not to contract and evolve at the rate of the Kelvin time-scale. And it is no use to put it back at the surface of the star—by bombarding the star with meteors, for example. It could not flow up the temperature-gradient, and so it would simply take the first opportunity of escaping as additional radiation. You cannot maintain a temperature-gradient by supplying heat at the bottom end. Heat must be poured in at the top end, i. e. in the deep interior of the star.
Since we cannot well imagine an extraneous source of heat able to release itself at the centre of a star, the idea of a star picking up energy as it goes along seems to be definitely ruled out. It follows that the star contains hidden within it the energy which has to last the rest of its life.
Energy has mass. Many people would prefer to say—energy is mass; but it is not necessary for us to discuss that. The essential fact is that an erg of energy in any form has a mass of 1·1. 10-21 grammes. The erg is the usual scientific unit of energy; but we can measure energy also by the gramme or the ton as we measure anything [Pg 97] else which possesses mass. There is no real reason why you should not buy a pound of light from an electric light company—except that it is a larger quantity than you are likely to need and at current rates would cost you something over £100,000,000. If you could keep all this light (ether-waves) travelling to and fro between mirrors forming a closed vessel, and then weigh the vessel, the observed weight would be the ordinary weight of the vessel plus 1 lb. representing the weight of the light. It is evident that an object weighing a ton cannot contain more than a ton of energy; and the sun with a mass of 2.000 quadrillion tons (p. 24) cannot contain more than 2.000 quadrillion tons of energy at the most.
Energy of 1·8. 1054 ergs has a mass 2. 1033 grammes which is the mass of the sun; consequently that is the sum total of the energy which the sun contains—the energy which has to last it all the rest of its life.[31] We do not know how much of this is capable of being converted into heat and radiation; if it is all convertible there is enough to maintain the sun’s radiation at the present rate for 15 billion years. To put the argument in another form, the heat emitted by the sun each year has a mass of 120 billion tons; and if this loss of mass continued there would be no mass left at the end of 15 billion years.
[Pg 98]
This store of energy is, with insignificant exception, energy of constitution of atoms and electrons; that is to say, subatomic energy. Most of it is inherent in the constitution of the electrons and protons—the elementary negative and positive electric charges—out of which matter is built; so that it cannot be set free unless these are destroyed. The main store of energy in a star cannot be used for radiation unless the matter composing the star is being annihilated.
It is possible that the star may have a long enough life without raiding the main energy store. A small part of the store can be released by a process less drastic than annihilation of matter, and this might be sufficient to keep the sun burning for 10,000,000,000 years or so, which is perhaps as long as we can reasonably require. The less drastic process is transmutation of the elements. Thus we have reached a point where a choice lies open before us; we can either pin our faith to transmutation of the elements, contenting ourselves with a rather cramped time-scale, or we can assume the annihilation of matter, which gives a very ample time-scale. But at present I can see no possibility of a third choice. Let me run over the argument again. First we found that energy of contraction was hopelessly inadequate; then we found that the energy must be released in the interior of the star, so that it comes from an internal, not an external, source; now we take stock of the whole internal store of energy. No supply of any importance is found until we come to consider the electrons and atomic nuclei; here a reasonable amount can be released by regrouping the protons and electrons in the atomic nuclei (transmutation of [Pg 99] elements), and a much greater amount by annihilating them.
Transmutation of the elements—so long the dream of the alchemist—is realized in the transformation of radio-active substances. Uranium turns slowly into a mixture of lead and helium. But none of the known radio-active processes liberate anything like enough energy to maintain the sun’s heat. The only important release of energy by transmutation occurs at the very beginning of the evolution of the elements.
We must start with hydrogen. The hydrogen atom consists simply of a positive and negative charge, a proton for the nucleus plus a planet electron. Let us call its mass 1. Four hydrogen atoms will make a helium atom. If the mass of the helium atom were exactly 4, that would show that all the energy of the hydrogen atoms remained in the helium atom. But actually the mass is 3·97; so that energy of mass a 0·03 must have escaped during the formation of helium from hydrogen. By annihilating 4 grammes of hydrogen we should have released 4 grammes of energy, but by transmuting it into helium we release 0·03 grammes of energy. Either process might be used to furnish the sun’s heat though, as we have already stated, the second gives a much smaller supply.
The release of energy occurs because in the helium atom only two of the four electrons remain as planet electrons, the other two being cemented with the four protons close together in the helium nucleus. In bringing positive and negative charges close together you cause a change of the energy of the electric field, and release electrical energy which spreads away as ether-waves. That is where the 0·03 grammes of energy has gone. The star can absorb these ether-waves and utilize them as heat.
[Pg 100]
We can go on from helium to higher elements, but we do not obtain much more release of energy. For example, an oxygen atom can be made from 16 hydrogen atoms or 4 helium atoms; but as nearly as we can tell it has just the weight of the 4 helium atoms, so that the release of energy is not appreciably greater when the hydrogen is transmuted into oxygen than when it is transmuted into helium.[32] This becomes clearer if we take the mass of a hydrogen atom to be 1·008, so that the mass of helium is exactly 4 and of oxygen 16; then it is known from Dr. Aston’s researches with the mass-spectrograph that the atoms of other elements have masses which are very closely whole numbers. The loss of 0·008 per hydrogen atom applies approximately whatever the element that is formed.
The view that the energy of a star is derived by the building up of other elements from hydrogen has the great advantage that there is no doubt about the possibility of the process; whereas we have no evidence that the annihilation of matter can occur in Nature. I am not referring to the alleged transmutation of hydrogen into helium in the laboratory; those whose authority I accept are not convinced by these experiments. To my mind the existence of helium is the best evidence we could desire of the possibility of the formation of helium. The four protons and two electrons constituting its nucleus must have been assembled at some time and place; and why not in the stars? When they were assembled the surplus energy must have been released, providing a prolific supply of heat. Prima facie this suggests the interior of a star as a likely locality, since undoubtedly a prolific source of heat is there in [Pg 101] operation. I am aware that many critics consider the conditions in the stars not sufficiently extreme to bring about the transmutation—the stars are not hot enough. The critics lay themselves open to an obvious retort; we tell them to go and find a hotter place.
But here the advantage seems to end. There are many astronomical indications that the hypothesis attributing the energy of the stars to the transmutation of hydrogen is unsatisfactory. It may perhaps be responsible for the rapid liberation of energy in the earliest (giant) stages when the star is a large diffuse body radiating heat abundantly; but the energy in later life seems to come from a source subject to different laws of emission. There is considerable evidence that as a star grows older it gets rid of a large fraction of the matter which originally constituted it, and apparently this can only be contrived by the annihilation of the matter. The evidence, however, is not very coherent, and I do not think we are in a position to come to a definite decision. On the whole the hypothesis of annihilation of matter seems the more promising; and I shall prefer it in the brief discussion of stellar evolution which I propose to give.
The phrase ‘annihilation of matter’ sounds like something supernatural. We do not yet know whether it can occur naturally or not, but there is no obvious obstacle. The ultimate constituents of matter are minute positive charges and negative charges which we may picture as centres of opposite kinds of strain in the ether. If these could be persuaded to run together they would cancel out, leaving nothing except a splash in the ether which spreads out as an electromagnetic wave carrying off the energy released by the undoing of the strain. The amount of this energy is amazingly large; by annihilating a single drop of water we [Pg 102] should be supplied with 200 horsepower for a year. We turn covetous eyes on this store without, however, entertaining much hope of ever discovering the secret of releasing it. If it should prove that the stars have discovered the secret and are using this store to maintain their heat, our prospect of ultimate success would seem distinctly nearer.
I suppose that many physicists will regard the subject of subatomic energy as a field of airy speculation. That is not the way in which it presents itself to an astronomer. If it is granted that the stars evolve much more slowly than on the contraction-hypothesis, the measurement of the output of subatomic energy is one of the commonest astronomical measurements—the measurement of the heat or light of the stars.[33] The collection of observational data as to the activity of liberation of subatomic energy is part of the routine of practical astronomy; and we have to pursue the usual course of arranging the measurements into some kind of coherence, so as to find out how the output is related to the temperature, density, or age of the material supplying it—in short, to discover the laws of emission. From this point onwards the discussion may be more or less hypothetical according to the temperament of the investigator; and indeed it is likely that in this as in other branches of knowledge advances may come by a proper use of the scientific imagination. Vain speculation is to be condemned in this as in any other subject, and there is no need for it; the problem is one of induction from observation with due regard to our [Pg 103] theoretical knowledge of the possibilities inherent in atomic structure.
I cannot pass from this subject without mentioning the penetrating radiation long known to exist in our atmosphere, which according to the researches of Kohlhörster and Millikan comes from outer space. Penetrating power is a sign of short wave-length and intense concentration of energy. Hitherto the greatest penetrating power has been displayed by Gamma rays originated by subatomic processes occurring in radio-active substances. The cosmic radiation is still more penetrating, and it seems reasonable to refer it to more energetic processes in the atom such as those suggested for the source of stellar energy. Careful measurements have been made by Millikan, and he concludes that the properties accord with those which should be possessed by radiation liberated in the transmutation of hydrogen; it is not penetrating enough to be attributed to a process so energetic as the annihilation of protons and electrons.
There seems to be no doubt that this radiation is travelling downwards from the sky. This is shown by measurements of its strength at different heights in the atmosphere and at different depths below the surface of mountain lakes; it is weakened according to the amount of air or water that it has had to traverse. Presumably its source must be extra-terrestrial. Its strength does not vary with the sun’s altitude, so it is not coming from the sun. There is some evidence that it varies according to the position of the Milky Way, most radiation being received when the greatest extension of the stellar system is overhead. It cannot come from the interior of the stars, the penetrating power being too limited; all the hottest and densest matter in the [Pg 104] universe is shut off from us by impenetrable walls. At the most it could come only from the outer rind of the stars where the temperature is moderate and the density is low; but it is more likely that its main source is in the diffuse nebulae or possibly in the matter forming the general cloud in space.[34]
We must await further developments before we can regard the supposed subatomic origin of this radiation as other than speculative; we mention it here only as a possible opening for progress. It will be of great interest if we can reach by this means a more direct acquaintance with the processes which we assume to be the source of stellar energy; and the messages borne to us by the cosmic rays which purport to relate to these processes deserve the closest attention. Our views of stellar energy are likely to be affected on one crucial point. Hitherto we have usually supposed that the very high temperature in the interior of a star is one of the essential conditions for liberation of subatomic energy, and that a reasonably high density is also important. Theoretically it would seem almost incredible that the building up of higher elements or the annihilation of protons and electrons could proceed with any degree of vigour in regions where encounters are rare and there is no high temperature or intense radiation to wake the atoms from apathy; but the more we face the difficulties of all theories of the release of subatomic energy the less inclined we are to condemn any evidence as incredible. The presence of sodium and calcium in the cosmical cloud, of helium and nebulium in the diffuse nebulae, [Pg 105] of titanium and zirconium in large quantities in the atmospheres of the youngest stars, bears witness that the evolution of the elements is already far advanced during the diffuse prestellar stage—unless indeed our universe is built from the debris of a former creation. From this point of view it is fitting that we should discern symptoms of subatomic activity in open space. But the physicist may well shake his head over the problem. How are four protons and two electrons to gather together to form a helium nucleus in a medium so rare that the free path lasts for days? The only comfort is that the mode of this occurrence is (according to present knowledge) so inconceivable under any conditions of density and temperature that we may postulate it in the nebulae—on the principle that we may as well be hung for a sheep as for a lamb.
Twenty years ago stellar evolution seemed to be very simple. The stars begin by being very hot and gradually cool down until they go out.
On this view the temperature of a star indicated the stage of evolution that it had reached. The outline of the sequence was sufficiently indicated by the crude observation of colour—white-hot, yellow-hot, red-hot; a more detailed order of temperature was ascertained by examining the light with a spectroscope. The red stars naturally came last in the sequence; they were the oldest stars on the verge of extinction. Sir Norman Lockyer strongly opposed this scheme and to a considerable extent anticipated the more modern view; but most astronomers pinned their faith to it up to about 1913.
Ten years ago more knowledge had been gained of the densities of [Pg 106] stars. It seemed likely that density would be a more direct criterion of evolutionary development than temperature. Granted that a star condenses out of nebulous material, it must in the youngest stage be very diffuse; from that stage it will contract and steadily increase in density.
But this necessitates an entire rearrangement of the scheme of evolution, because the order according to density is by no means the same as the order according to surface temperature. On the former view all the cool red stars were old and dying. But a large number of them are now found to be extremely diffuse—stars like Betelgeuse, for instance. These must be set down as the very youngest of the stars; after all it is not unnatural that a star just beginning to condense out of nebulous material should start at the lowest stage of temperature. Not all the red stars are diffuse; there are many like Krueger 60 which have high density, and these we leave undisturbed as representing the last stage of evolution. Both the first and last periods of a star’s life are characterized by low temperature; in between whiles the temperature must have risen to a maximum and fallen again.
The ‘giant and dwarf theory’ proposed by Hertzsprung and Russell brought these conclusions into excellent order. It recognized a series of giant stars, comparatively diffuse stars with temperature rising, and a series of dwarf or dense stars with temperature falling. The two series merged at the highest temperatures. An individual star during its lifetime went up the giant series to its highest temperature and then down the dwarf series. The brightness remained fairly steady throughout the giant stage because the continually increasing temperature counterbalanced the reduction of the surface area of the star; in the dwarf stage the decreasing [Pg 107] temperature and the contraction of the surface caused a rapid decrease of brightness as the star progressed down the series. This was in accordance with observation. The theory has dominated most recent astrophysical research and has been instrumental in bringing to light many important facts. One example must suffice. Although we may have a giant and a dwarf star with the same surface temperature, and therefore showing very similar spectra, nevertheless a close examination of the spectrum reveals tell-tale differences; and it is now quite easy to ascertain from the spectrum whether the star is a diffuse giant or a dense dwarf.
The attractive feature of the giant and dwarf theory was the simple explanation given for the up-and-down progress of the temperature. The passing over from the giant to the dwarf series was supposed to occur when the density had reached such a value (about one-quarter the density of water) that the deviation of the material from a perfect gas began to be serious. It was shown by Lane fifty years ago that a globe of perfect gas must rise in temperature as it contracts, his method of finding the internal temperature being that considered on p. 12; thus the rising temperature in the giant stage is predicted. But the rise depends essentially on the easy compressibility of the gas; and when the compressibility is lost at high density the rising temperature may be expected to give place to falling temperature so that the star cools as a solid or liquid would do. That was believed to account for the dwarf stage.
I have been trying to recall ideas of twenty and ten years ago, and you must not suppose that from the standpoint of present-day knowledge I can endorse everything here stated. I have intentionally been vague [Pg 108] as to whether by the hotness of a star I mean the internal or the surface temperature since ideas were formerly very loose on this point; I have made no reference to white dwarfs, which are now thought to be the densest and presumably the oldest stars of all. But it is the last paragraph especially which conflicts with our latest conclusions, for we no longer admit that stellar material will cease to behave as a perfect gas at one-quarter the density of water. Our result that the material in the dense dwarf stars is still perfect gas (p. 38) strikes a fatal blow at this part of the giant and dwarf theory.
It would be difficult to say what is the accepted theory of stellar evolution to-day. The theory is in the melting-pot and we are still waiting for something satisfactory to emerge. The whole subject is in doubt and we are prepared to reconsider almost anything. Provisionally, however, I shall assume that the former theory was right in assuming that the sequence of evolution is from the most diffuse to the densest stars. Although I make this assumption I do not feel sure that it is allowable. The former theory had strong reasons for making it which no longer apply. So long as contraction was supposed to be the source of a star’s heat, contraction and increasing density were essential throughout its whole career; with the acceptance of subatomic energy contraction ceases to play this fundamental role.
I propose to confine attention to the dwarf stars[35] because it is among them that the upset has occurred. They form a well-defined series stretching from high surface-temperature to low surface-temperature, high luminosity to low luminosity, and the density increases steadily [Pg 109] along the series. We now call this the Main Series. It comprises the great majority of the stars. To fix ideas let us take three typical stars along the series—Algol near the top, the Sun near the middle, and Krueger 60 near the bottom. The relevant information about them is summarized below:
| Star. | Mass (Sun = 1). |
Mean density (Water =1) |
Central temperature (million deg.). |
Surface temperature (deg.). |
Colour. | Luminosity (Sun = 1). |
|---|---|---|---|---|---|---|
| Algol | 4·3 | 0·15 | 40 | 12,000 | white | 150 |
| Sun | 1 | 1·4 | 40 | 6,000 | yellow | 1 |
| Krueger 60 | 0·27 | 9·1 | 35 | 3,000 | red | 0·01 |
The idea of evolution is that these represent the stages passed through in the life-history of an individual star.[36] The increasing density in the third column should be noticed; according to our accepted criterion it indicates that the order of development is Algol→Sun→Krueger 60. A confusion between internal temperature and surface temperature is responsible for some of the mistakes of the older theories. To outward view the star cools from 12,000° to 3,000° in passing down the series, but there is no such change in its internal heat. The central temperature remains surprisingly steady. (No special [Pg 110] reliance can be placed on the slight falling off apparently shown by Krueger 60.) It is very remarkable that all stars of the main series have a central temperature of about 40 million degrees as nearly as we can calculate. It is difficult to resist the impression that there is some unusual property associated with this temperature, although all our physical instincts warn us that the idea is absurd.
But the vital point is the decrease of mass shown in the second column. If an individual star is to progress any part of the way down the main series it must lose mass. We can put the same inference in a more general way. Now that it has been found that luminosity depends mainly on mass, there can be no important evolution of faint stars from bright stars unless the stars lose a considerable part of their mass.
It is this result which has caused the hypothesis of annihilation of matter to be seriously discussed. All progress in the theory of stellar evolution is held up pending a decision on this hypothesis. If it is accepted it provides an easy key to these changes. The star may (after passing through the giant stage) reach the stage of Algol, and then by the gradual annihilation of the matter in it pass down the main series until when only one-sixteenth of the original mass remains it will be a faint red star like Krueger 60. But if there is no annihilation of matter, the star when once it has reached the dwarf stage seems to be immovable; it has to stay at the point of the series corresponding to its constant mass.
Let it be clearly understood what is the point at issue. The stars lose mass by their radiation; there is no question about that. The sun is losing 120 billion tons annually whether its radiation comes from annihilation of matter or any other internal source. The question is, How long can this loss continue? Unless there is annihilation of [Pg 111] matter, all the mass that can escape as radiation will have escaped in a comparatively short time; the sun will then be extinct and there is an end to the loss and to the evolution. But if there is annihilation of matter the life of the sun and the loss of mass continue far longer, and an extended track of evolution lies open before the sun; when it has got rid of three-quarters of its present mass it will have become a faint star like Krueger 60.
Our choice between the possible theories of subatomic energy only affects stellar evolution in one point—but it is the vital point. Unless we choose annihilation of matter, we cut the life of a star so short that there is no time for any significant evolution at all.
I feel the same objection that every one must feel to building extensively on a hypothetical process without any direct evidence that the laws of Nature permit of its occurrence. But the alternative is to leave the stars in sleepy uniformity with no prospect of development or change until their lives come to an end. Something is needed to galvanize the scene into that activity, whether of progress or decay, in which we have so long believed. Rather desperately we seize on the one visible chance. The petrified system wakes. The ultimate particles one by one yield up their energy and pass out of existence. Their sacrifice is the life-force of the stars which now progress on their high adventure:
[Pg 112]
Our first evidence of the extent of the time-scale of stellar evolution was afforded by the steadiness of condition of δ Cephei. This was supplemented by evidence of the great extension of geological time on the earth. We could not do more than set an upper limit to the rate of progress of evolution and a lower limit to the age of the stars. But this limit was sufficient to rule out the contraction hypothesis and drive us to consider the store of subatomic energy.
We now make a new attack, which depends on the belief that the rate of evolution is determined by the rate at which a star can get rid of its mass. We are here considering only the evolution of faint stars from bright stars, and there will remain scope for a certain amount of development in the giant stage to which our arguments will not directly apply. But to abandon all lines of evolution between bright stars and faint stars would mean admitting that one star differs from another star in brightness because it was different originally. This may be true; but we ought not to surrender the main field of stellar evolution without making a fight for it.
By the new line of attack we reach a definite determination of the time-scale and not merely a lower limit. We know the rate at which stars in each stage are losing mass by radiation; therefore we can find the time taken to lose a given mass and thereby pass on to a stage of smaller mass. Evolution from Algol to the Sun requires five billion years; evolution from the Sun to Krueger 60 requires 500 billion years. It is interesting to note that stars in the stage between the Sun and Krueger 60 are much more abundant than those between Algol and the Sun—a fact somewhat confirmatory of the calculated duration of the [Pg 113] two stages. The abundance of faint stars does not, however, increase so rapidly as the calculated duration; perhaps the stellar universe has not existed long enough for the old stars to be fully represented.
A star of greater mass than Algol squanders its mass very rapidly, so that we do not increase the age of the Sun appreciably by supposing it to have started with greater mass than Algol. The upper limit to the present age of the Sun is 5·2 billion years however great its initial mass.
But, it may be asked, cannot a star accelerate its progress by getting rid of matter in some other way than by radiation? Cannot atoms escape from its surface? If so the loss of mass and consequent evolution will be speeded up, and the time required may perhaps even be brought within range of the alternative theory of transmutation of the elements. But it is fairly certain that the mass escaping in the form of material atoms is negligible compared with that which imperceptibly glides away in the form of radiation. You will perhaps be in doubt as to whether the 120 billion tons per annum lost by the sun in radiation is (astronomically regarded) a large quantity or a small quantity. From certain aspects it is a large quantity. It is more than 100,000 times the mass of the calcium chromosphere. The sun would have to blow off its chromosphere and form an entirely fresh one every five minutes in order to get rid of as much mass in this way as it loses by radiation. It is obvious from solar observation that there is no such outrush of material. To put it another way—in order to halve the time-scale of evolution stated above it would be necessary that a billion atoms should escape each second through each square centimetre of the sun’s surface. I think we may conclude that there is no short cut to smaller [Pg 114] mass and that radiation is responsible for practically the whole loss.
We noticed earlier (p. 25) that Nature builds stars which are much alike in mass, but allows herself some deviation from her pattern amounting sometimes to a mistake of one 0. I think we may have done her an injustice, and that she is more careful over her work than we supposed. We ought to have examined coins fresh from her mint; it was not fair to take coins promiscuously, including many that had been in circulation for some hundreds of billions of years and had worn rather thin. Taking the newly formed stars, i. e. the diffuse stars, we find that 90 per cent. of them are between 2½ and 5½ times the mass of the sun—showing that initially the stars are made nearly as closely to pattern as human beings are. In this range radiation pressure increases from 17 to 35 per cent, of the whole pressure; I think this would be expected to be the crucial stage in its rise to importance. Our idea is that the stellar masses initially have this rather close uniformity (which does not exclude a small proportion of exceptional stars outside the above limits); the smaller masses are evolved from these in course of time by the radiation of mass.
For the time being the sun is comfortably settled in its present state, the amount of energy radiated being just balanced by the subatomic energy liberated inside it. Ultimately, however, it must move on. The moving on, or evolution, is continuous, but for convenience of explanation we shall speak of it as though it occurred in steps. Two possible motives for change can be imagined, (1) the supply of subatomic energy might fall off by exhaustion and no longer balance the radiation, and (2) the sun is slowly becoming a star of smaller mass. In former theories the first motive has generally been assumed, and we [Pg 115] may still regard it as effective during the giant stage of the stars; but it is clear that the motive to move down the main series must be loss of mass.[37] Apparently the distinction between giant and dwarf stars, replacing the old distinction of perfect and imperfect gas, is that the prolific and soon exhausted supplies of subatomic energy in the giant stage disappear and leave a much steadier supply in the dwarf stage.
When the sun has become a star of smaller mass it will need to resettle its internal conditions. Suppose that at first it tries to retain its present density. As explained on p. 12, we can calculate the internal temperature, and we find that the reduced mass coupled with constant density involves lower temperature. This will slightly turn off the tap of subatomic energy, because there can be little doubt that the release of subatomic energy is more rapid at higher temperature. The reduced supply will no longer be sufficient to balance the radiation; accordingly the star will contract just as it was supposed to do on the old contraction hypothesis which corresponds to the tap of subatomic energy being turned off altogether. The motive is loss of mass; the first consequence is an increase of density which is another characteristic of progress down the main series.
Tracing the consequences a little farther, the increasing density causes a rising temperature which in turn reopens the tap of subatomic energy. As soon as the tap is opened enough to balance the rate of radiation of the star, the contraction stops and the star remains settled in equilibrium at the smaller mass and higher density.
[Pg 116]
You will see that the laws of release of subatomic energy must be invoked if we are to explain quantitatively why a particular density corresponds to a particular mass in the progress down the main series. The contraction has to proceed so far as to bring the internal conditions to a state in which the release of energy is at the exact rate required to balance the radiation.
I am afraid this all sounds very complicated, but my purpose is to show that the adjustment of the star after an alteration of mass is automatic. After a change of mass the star has to re-solve the problem of the internal conditions necessary for its equilibrium. So far as mechanical conditions are concerned (supporting the weight of the upper layers) it can choose any one of a series of states of different density provided it has the internal temperature appropriate to that density. But such equilibrium is only temporary, and the star will not really settle down until the tap of subatomic energy is opened to the right extent to balance the rate of radiation which, as we have already seen, is practically fixed by the mass. The star fiddles about with the tap until it secures this balance.
One important conclusion has been pointed out by Professor Russell. When the star is adjusting the tap it does not do so intelligently; one trial must automatically lead to the next trial, and it is all-important that the next trial should automatically be nearer to and not farther from the right rate. The condition that it shall be nearer to the right rate is that the liberation of subatomic energy shall increase with temperature or density.[38] If it decreases, or even if it is unaltered, the trials will be successively farther [Pg 117] and farther from the required rate, so that although a steady balance is possible the star will never be able to find it. It is therefore essential to admit as one of the laws of liberation of subatomic energy that the rate increases with temperature or with density or with both; otherwise subatomic energy will not fulfil the purpose for which it was introduced, viz. to keep the star steady for a very long time.
The strange thing is that the condition of balance is reached when the central temperature is near 40 million degrees—the same whether the star is at the top, middle, or bottom of the main series. Stars at the top release from each gramme of material 700 ergs of energy per second; the sun releases 1 ergs per second; Krueger 60 releases 0·08 ergs per second. It seems extraordinary that stars requiring such different supplies should all have to ascend to the same temperature to procure them. It looks as though at temperatures below this standard not even 0·08 ergs per second is available, but on reaching the standard the supply is practically unlimited. We can scarcely believe that there is a kind of boiling-point (independent of pressure) at which matter boils off into energy. The whole phenomenon is most perplexing.
I may add that the giant stars have temperatures considerably below 40 million degrees. It would appear that they are tapping special supplies of subatomic energy released at lower temperatures. After using up these supplies the star passes on to the main series, and proceeds to tap the main supply. It seems necessary to suppose further that the main supply does not last indefinitely, so that ultimately the star (or what is left of it) leaves the main series and passes on to the white dwarf stage.
We are now in a position to deal with a question which you may [Pg 118] have wished to ask earlier. Why does δ Cephei pulsate? One possible answer is that the oscillation was started off by some accident. So far as we can calculate an oscillation, if once started, would continue for something like 10,000 years before becoming damped down. But 10,000 years is now deemed to be an insignificant period in the life of a star, and, having regard to the abundance of Cepheids, the explanation seems inadequate even if we could envisage the kind of accident supposed. It is much more likely that the pulsation arises spontaneously. Enormous supplies of heat energy are being released in the star—far more than enough to start and maintain the pulsation—and there are at least two alternative ways in which this heat can be supposed to operate a mechanism of pulsation.
Here is one alternative. Suppose first that there is a very small pulsation. When compressed the star has higher temperature and density than usual and the tap of subatomic energy is opened more fully. The star gains heat, and the expansive force of the extra heat assists the rebound from compression. At greatest expansion the tap is turned off a little and the loss of heat diminishes the resistance to the ensuing compression. Thus the successive expansions and compressions become more and more vigorous and a large pulsation grows out of an infinitesimal beginning. It will be seen that the star works the tap of subatomic energy just as an engine works the valve admitting heat into its cylinder; so that the pulsations of a star are started up like the pulsations of an engine.
The only objection that I can find to this explanation is that it is too successful. It shows why a star may be expected to pulsate; but the trouble is that stars in general do not pulsate—it is only [Pg 119] the rare exceptions that behave in this way. It is now so easy to account for the Cepheids that we have to turn back and face the more difficult problem of accounting for the normal steady stars. Whether the pulsation will start up or not depends on whether the engine of pulsation is sufficiently powerful to overcome the forces tending to damp out and dissipate pulsations. We cannot predict the occurrence or non-occurrence from any settled theory; we have rather to seek to frame the laws of release of subatomic energy so as to conform to our knowledge that the majority of the stars remain steady, but certain conditions of mass and density give the pulsatory forces the upper hand.
Cepheid pulsation is a kind of distemper which happens to stars at a certain youthful period; after passing through it they burn steadily. There may be another attack of disease later in life when the star is subject to those catastrophic outbursts which occasion the appearance of ‘new stars’ or novae. But very little is known as to the conditions for this, and it is not certain whether the outbreak is spontaneous or provoked from outside.
So long as we stick to generalities the theory of subatomic energy and especially the theory of annihilation of matter makes a fairly promising opening. It is when we come to technical details that doubts and perplexities arise. Difficulties appear in the simultaneous presence of giant and dwarf stars in coeval clusters, notwithstanding their widely different rates of evolution. There are difficulties in devising laws of release of subatomic energy which will safeguard the stability of the stars without setting every star into pulsation. Difficulties arise from the fact that as a rule in the giant stage the lower the temperature and density the more rapid the release of energy; and although we account for this in a general way by considering the [Pg 120] exhaustibility of the more prolific sources of energy, the facts are not all straightened out by such a scheme. Finally grave difficulties arise in reconciling the laws of release inferred from astronomical observation with any theoretical picture we can form of the process of annihilation of matter by the interplay of atoms, electrons, and radiation.
The subject is highly important, but we cannot very well pursue it further in this lecture. When the guidance of theory is clear interest centres round the broad principles; when the theory is rudimentary, interest centres round technical details which are anxiously scrutinized as they appear to favour now one view now another. I have dealt mainly with two salient points—the problem of the source of a star’s energy and the change of mass which must occur if there is any evolution of faint stars from bright stars. I have shown how these appear to meet in the hypothesis of annihilation of matter. I do not hold this as a secure conclusion. I hesitate even to advocate it as probable, because there are many details which seem to me to throw considerable doubt on it, and I have formed a strong impression that there must be some essential point which has not yet been grasped. I simply tell it you as the clue which at the moment we are trying to follow up—not knowing whether it is false scent or true.
I should have liked to have closed these lectures by leading up to some great climax. But perhaps it is more in accordance with the true conditions of scientific progress that they should fizzle out with a glimpse of the obscurity which marks the frontiers of present knowledge. I do not apologize for the lameness of the conclusion, for it is not a conclusion. I wish I could feel confident that it is even a beginning.
[Pg 121]
[1] Fig. 1 is from a photograph taken by Mr. Evershed at Kodaikanal Observatory, Madras. Fig. 2 is from the Mount Wilson Observatory, California.
[3] Primarily it is the electric charge and not the high speed of particles which determines their appearance in these photographs. But a high-speed particle leaves behind it a trail of electrically charged particles—the victims of its furious driving—so that it is shown indirectly by its line of victims.
[4] Other substitutions for silver do not as a rule cause greater change, and the differences are likely to be toned down by mixture of many elements. Excluding hydrogen, the most extreme change is from 48 particles for silver to 81 particles for an equal mass of helium. But for hydrogen the change is from 48 to 216, so that hydrogen gives widely different results from other elements.
[5] The mean density of Capella is nearly the same as the density of the air.
[6] Unless otherwise indicated ‘gaseous’ is intended to mean ‘composed of perfect gas’.
[7] For this prediction it is unnecessary to know the chemical composition of the stars, provided that extreme cases (e. g. an excessive proportion of hydrogen) are excluded. For example, consider the hypotheses that Capella is made respectively of (a) iron, (b) gold. According to theory the opacity of a star made of the heavier element would be 2½ times the opacity of a star made of iron. This by itself would make the golden star a magnitude (= 2½ times) fainter. But the temperature is raised by the substitution; and although, as explained on p. 23, the change is not very great, it increases the outflow of heat approximately 2½ times. The resultant effect on the brightness is practically no change. Whilst this independence of chemical constitution is satisfactory in regard to definiteness of the results, it makes the discrepant factor 10 particularly difficult to explain.
[8] Observation shows that the sun is about 4 magnitudes fainter than the average diffuse star of the same spectral class, and Krueger 60 is 10 magnitudes fainter than diffuse stars of its class. The whole drop was generally assumed to be due to deviation from a perfect gas; but this made no allowance for a possible difference of mass. The comparison with the curve enables the dense star to be compared with a gaseous star of its own mass, and we see that the difference then disappears. So that (if there has been no mistake) the dense star is a gaseous star, and the differences above mentioned were due wholly to differences of mass.
[9] Rougher estimates were made much earlier.
[10] The observed period of Algol is the period of revolution, not of rotation. But the two components are very close together, and there can be no doubt that owing to the large tidal forces they keep the same faces turned towards each other; that is to say, the periods of rotation and of revolution are equal.
[11] It may be of interest to add that although the proper light of Algol B is inappreciable, we can observe a reflection (or re-radiation) of the light of Algol A by it. This reflected light changes like moonlight according as Algol B is ‘new’ or ‘full’.
[11] The mass-luminosity relation was not suspected at the time of which I am speaking.
[13] My references to ‘perfect gas of the density of platinum’ and ‘material 2,000 times denser than platinum’ have often been run together by reporters into ‘perfect gas 2,000 times denser than platinum’. It is scarcely possible to calculate what is the condition of the material in the Companion of Sirius, but I do not expect it to be a perfect gas.
[14] Photographed by Dr. W. H. Wright at the Lick Observatory, California.
[15] Nos. 43, 61, 75 are recent discoveries and may require confirmation. There now remain only two gaps (85 and 87) apart from possible elements beyond uranium.
[16] It does not give both temperature and pressure, but it gives one if the other is known. This is valuable information which may be pieced together with other knowledge of the conditions at the surface of the stars.
[17] Hydrogen (being element No. 1) has only one planet electron.
[18] Fig. 9 is a photograph of the ‘flash spectrum’ of the sun’s chromosphere taken by Mr. Davidson in Sumatra at the eclipse of 14 January 1926.
[19] The helium line in the Ring Nebula on which we have already commented is not a member of the Pickering Series, but it has had the same history. It was first supposed to be due to hydrogen, later (in 1912) reproduced by Fowler terrestrially in a mixture of helium and hydrogen, and finally discovered by Bohr to belong to helium.
[20] This, of course, is found from the other lines of the spectrum which genuinely belong to the star and shift to and fro as it describes its orbit.
[21] As the word temperature is sometimes used with new-fangled meanings, I may add that 15,000° is the temperature corresponding to the individual speeds of the atoms and electrons—the old-fashioned gas-temperature.
[22] Photograph taken by E. T. Cottingham and the author in Principe at the total eclipse of 29 May 1919.
[23] We refer to calcium as it occurs in the chromosphere, i. e. with one electron missing.
[24] There is an awkwardness in applying the term ‘apparent’ to something too small to be seen; but, remembering that we have armed ourselves with an imaginary telescope capable of showing the disk, the meaning will be clear.
[25] Densities below that of air have been found for some of the Algol variables by an entirely different kind of investigation, and also for some of the Cepheid variables by still another method. There are also many other examples of stars of bulk comparable with that of Betelgeuse.
[26] From a photograph taken at the Royal Observatory, Cape of Good Hope.
[27] For comparison, the nearest fixed star is distant 4 light years. Apart from clusters we rarely deal with distances above 2,000 light years.
[28] One cannot always be sure that what is true of the cluster stars will be true of stars in general; and our knowledge of the nearer stars, though lagging behind that of the stars in clusters, does not entirely agree with this association of colour and brightness.
[29] The term nebula covers a variety of objects, and it is only the nebulae classed as spirals that are likely to be outside our stellar system.
[30] This can be checked because uranium lead has a different atomic weight from lead not so derived. Ordinary lead is a mixture of several kinds of atoms (isotopes).
[31] You may wonder why, having said that the sun contains 2,000 quadrillion tons of energy at the most, I now assume that it contains just this amount. It is really only a verbal point depending on the scientific definition of energy. All mass is mass of something, and we now call that something ‘energy’ whether it is one of the familiar forms of energy or not. You will see in the next sentence that we do not assume that the energy is convertible into known forms, so that it is a terminology which commits us to nothing.
[32] Aston in his latest researches has been able to detect that the oxygen atom is just appreciably lighter than the four helium atoms.
[33] A measurement of the heat observed to flow from a continuous fountain of heat is a measurement of the output of the fountain, unless there is a storing of energy between the output and the outflow. The breakdown of the Kelvin time-scale indicates that the storing in the stars (positive or negative) and consequent expansion or contraction is negligible compared to the output or outflow.
[34] The stars all put together cover an area of the sky much less than the apparent disk of the sun, so that unless their surface-layers are generating this radiation very much more abundantly than the sun does, they cannot be responsible for it.
[35] The term ‘dwarf stars’ is not meant to include white dwarfs.
[36] We can scarcely suppose that all stars after reaching the main series pass through precisely the same stages. For example, Algol, when it has become reduced to the mass of the Sun, may have slightly different density and temperature. But the observational evidence indicates that these individual differences are small. The main series is nearly a linear sequence; it must have some ‘breadth’ as well as ‘length’, but at present the scatter of the individual stars away from the central line of the sequence seems to be due chiefly to the probable errors of the observational data and the true breadth has not been determined.
[37] Exhaustion of supply without change of mass would cause the star to contract to higher density; it would thus have a combination of density and mass which (according to observation) is not found in any actual stars.
[38] This increase was assumed in our detailed description of the automatic adjustment of the star, and it will be seen that it was essential to assume it.
I HAVE preferred not to complicate the Story of the Companion of Sirius with details of a technical kind; some further information may, therefore, be welcome to those readers who are curious to learn as much as possible about this remarkable star. I am also able to add a further instalment of the ‘detective story’ which has just come to hand, the sleuth this time being Mr. R. H. Fowler.
The star is between the eighth and ninth magnitude, so that it is not an excessively faint object. The difficulty in detecting it arises entirely from the overpowering light of its neighbour. At favourable epochs it has been seen easily with an 8-inch telescope. The period of revolution is 49 years.
The Companion is separated from Sirius by a distance nearly equal to the distance of Uranus from the Sun—or twenty times the earth’s distance from the sun. It has been suggested that the light might be reflected light from Sirius. This would account for its whiteness, but would not directly account for its spectrum, which differs appreciably from that of Sirius. To reflect ¹⁄₁₀₀₀₀th of the light of Sirius (its actual brightness) the Companion would have to be 74 million miles in diameter. The apparent diameter of its disk would be 0"·3, which, one would think, could scarcely escape notice in spite of unfavourable conditions of observation. But the strongest objection to this hypothesis of reflected light is that it applies only to this one star. The other two recognized white dwarfs have no brilliant star in their neighbourhood, so that they cannot be shining by reflected light. It is scarcely worth while to invent an elaborate explanation for one of these strange objects which does not cover the other two.
The Einstein effect, which is appealed to for confirmation of the high density, is a lengthening of the wave-length and corresponding decrease of the frequency of the light due to the intense gravitational field through which the rays have to pass. Consequently the dark lines in the spectrum appear at longer wave-lengths, i.e. displaced towards the red as compared with the corresponding terrestrial lines. The effect can be deduced either from the relativity theory of gravitation or from the [Pg 122] quantum theory; for those who have some acquaintance with the quantum theory the following reasoning is probably the simplest. The stellar atom emits the same quantum of energy hν as a terrestrial atom, but this quantum has to use up some of its energy in order to escape from the attraction of the star; the energy of escape is equal to the mass hν/c2 multiplied by the gravitational potential Φ at the surface of the star. Accordingly the reduced energy after escape is hν(1 - Φ/c2); and since this must still form a quantum hν', the frequency has to change to a value ν' = ν(1 - Φ/c2). Thus the displacement ν' - ν is proportional to Φ, i.e. to the mass divided by the radius of the star.
The effect on the spectrum resembles the Doppler effect of a velocity of recession, and can therefore only be discriminated if we know already the line-of-sight velocity. In the case of a double star the velocity is known from observation of the other component of the system, so that the part of the displacement attributable to Doppler effect is known. Owing to orbital motion there is a difference of velocity between Sirius and its Companion amounting at present to 43 km. per sec. and this has been duly taken into account; the observed difference in position of the spectral lines of Sirius and its Companion corresponds to a velocity of 23 km. per sec. of which 4 km. per sec. is attributable to orbital motion, and the remaining 19 km. per sec. must be interpreted as Einstein effect. The result rests mainly on measurements of one spectral line Hβ. The other favourable lines are in the bluer part of the spectrum, and since atmospheric scattering increases with blueness, the scattered light of Sirius interferes. However, they afford some useful confirmatory evidence.
Of the other white dwarfs ο2 Eridani is a double star, its companion being a red dwarf fainter than itself. The red shift of the spectrum will be smaller than in the Companion of Sirius and it will not be so easy to separate it from various possible sources of error. Nevertheless the prospect is not hopeless. The other recognized white dwarf is an unnamed star discovered by Van Maanen; it is a solitary star, and consequently there is no means of distinguishing between Einstein shift and Doppler shift. Various other stars have been suspected of being in this condition, including the Companions of Procyon, 85 Pegasi, and Mira Ceti.
[Pg 123]
If the Companion of Sirius were a perfect gas its central temperature would be about 1,000,000,000°, and the central part of the star would be a million times as dense as water. It is, however, unlikely that the condition of a perfect gas continues to hold. It should be understood that in any case the density will fall off towards the outside of the star, and the regions which we observe are entirely normal. The dense material is tucked away under high pressure in the interior.
Perhaps the most puzzling feature that remains is the extraordinary difference of development between Sirius and its Companion, which must both have originated at the same time. Owing to the radiation of mass the age of Sirius must be less than a billion years; an initial mass, however large, would radiate itself down to less than the present mass of Sirius within a billion years. But such a period is insignificant in the evolution of a small star which radiates more slowly, and it is difficult to see why the Companion should have already left the main series and gone on to this (presumably) later stage. This is akin to other difficulties in the problem of stellar evolution, and I feel convinced that there is something of fundamental importance that remains undiscovered.
Until recently I have felt that there was a serious (or, if you like, a comic) difficulty about the ultimate fate of the white dwarfs. Their high density is only possible because of the smashing of the atoms, which in turn depends on the high temperature. It does not seem permissible to suppose that the matter can remain in this compressed state if the temperature falls. We may look forward to a time when the supply of subatomic energy fails and there is nothing to maintain the high temperature; then on cooling down, the material will return to the normal density of terrestrial solids. The star must, therefore, expand, and in order to regain a density a thousandfold less the radius must expand tenfold. Energy will be required in order to force out the material against gravity. Where is this energy to come from? An ordinary star has not enough heat energy inside it to be able to expand against gravitation to this extent; and the white dwarf can scarcely be supposed to have had sufficient foresight to make special provision for this remote demand. Thus the star may be in an awkward predicament—it will be losing heat continually but will not have enough energy to cool down.
[Pg 124]
One suggestion for avoiding this dilemma is like the device of a novelist who brings his characters into such a mess that the only solution is to kill them off. We might assume that subatomic energy will never cease to be liberated until it has removed the whole mass—or at least conducted the star out of the white dwarf condition. But this scarcely meets the difficulty; the theory ought in some way to guard automatically against an impossible predicament, and not to rely on disconnected properties of matter to protect the actual stars from trouble.
The whole difficulty seems, however, to have been removed in a recent investigation by R. H. Fowler. He concludes unexpectedly that the dense matter of the Companion of Sirius has an ample store of energy to provide for the expansion. The interesting point is that his solution invokes some of the most recent developments of the quantum theory—the ‘new statistics’ of Einstein and Bose and the wave-theory of Schrödinger. It is a curious coincidence that about the time that this matter of transcendently high density was engaging the attention of astronomers, the physicists were developing a new theory of matter which specially concerns high density. According to this theory matter has certain wave properties which barely come into play at terrestrial densities; but they are of serious importance at densities such as that of the Companion of Sirius. It was in considering these properties that Fowler came upon the store of energy that solves our difficulty; the classical theory of matter gives no indication of it. The white dwarf appears to be a happy hunting ground for the most revolutionary developments of theoretical physics.
To gain some idea of the new theory of dense matter we can begin by referring to the photograph of the Balmer Series in Fig. 9. This shows the light radiated by a large number of hydrogen atoms in all possible states up to No. 30 in the proportions in which they occur naturally in the sun’s chromosphere. The old-style electromagnetic theory predicted that electrons moving in curved paths would radiate continuous light; and the old-style statistical theory predicted the relative abundance of orbits of different sizes, so that the distribution of light along this continuous spectrum could be calculated. These predictions are wrong and do not give the distribution of light shown in the photograph; but they become less glaringly wrong as we draw [Pg 125] near to the head of the series. The later lines of the series crowd together and presently become so close as to be practically indistinguishable from continuous light. Thus the classical prediction of continuous spectrum is becoming approximately true; simultaneously the classical prediction of its intensity approaches the truth. There is a famous Correspondence Principle enunciated by Bohr which asserts that for states of very high number the new quantum laws merge into the old classical laws. If we never have to consider states of low number it is indifferent whether we calculate the radiation or statistics according to the old laws or the new.
In high-numbered states the electron is for most of the time far distant from the nucleus. Continuous proximity to the nucleus indicates a low-numbered state. Must we not expect, then, that in extremely dense matter the continuous proximity of the particles will give rise to phenomena characteristic of low-numbered states? There is no real discontinuity between the organization of the atom and the organization of the star; the ties which bind the particles in the atom, bind also more extended groups of particles and eventually the whole star. So long as these ties are of high quantum number, the alternative conception is sufficiently nearly valid which represents the interactions by forces after the classical fashion and takes no cognizance of ‘states’. For very high density there is no alternative conception, and we must think not in terms of force, velocity, and distribution of independent particles, but in terms of states.
The effect of this breakdown of the classical conception can best be seen by passing at once to the final limit when the star becomes a single system or molecule in state No. 1. Like an excited atom collapsing with discontinuous jumps such as those which give the Balmer Series, the star with a few last gasps of radiation will reach the limiting state which has no state beyond. This does not mean that further contraction is barred by the ultimate particles jamming in contact, any more than collapse of the hydrogen atom is barred by the electron jamming against the proton; progress is stopped because the star has got back to the first of an integral series of possible conditions of a material system. A hydrogen atom in state No. 1 cannot radiate; nevertheless its electron is moving with high kinetic energy. [Pg 126] Similarly a star when it has reached state No. 1 no longer radiates; nevertheless its particles are moving with extremely great energy. What is its temperature? If you measure temperature by radiating power its temperature is absolute zero, since the radiation is nil; if you measure temperature by the average speed of molecules its temperature is the highest attainable by matter. The final fate of the white dwarf is to become at the same time the hottest and the coldest matter in the universe. Our difficulty is doubly solved. Because the star is intensely hot it has enough energy to cool down if it wants to; because it is so intensely cold it has stopped radiating and no longer wants to grow any colder.
We have described what is believed to be the final state of the white dwarf and perhaps therefore of every star. The Companion of Sirius has not yet reached this state, but it is so far on the way that the classical treatment is already inadmissible. If any stars have reached state No. 1 they are invisible; like atoms in the normal (lowest) state they give no light. The binding of the atom which defies the classical conception of forces has extended to cover the star. I little imagined when this survey of Stars and Atoms was begun that it would end with a glimpse of a Star-Atom.
[Pg 127]
Printed in England at the OXFORD UNIVERSITY PRESS
by John Johnson Printer to the University